A. GENERALITES
Résumé — Ce chapitre expose succinctement les propriétés de l'atmosphère quant à la transmission des ondes infrarouges et des hyperfréquences. Les raies d'absorption des composants atmosphériques sont très nombreuses dans le domaine infrarouge, beaucoup moins dans le domaine des micro-ondes : vers 22, 60, 118 et 183 GHz pour ce dernier. L'effet des nuages est beaucoup plus sensible pour le premier domaine. Dans une deuxième section sont présentées les lois de Planck et de Rayleigh-Jeans et quelques notions inhérentes aux définitions de température de bruit et de sensibilité radiométrique.
1. L'ATMOSPHERE ET LE SPECTRE ELECTROMAGNETIQUE
L'atmosphère terrestre est tout à fait opaque pour l'essentiel du spectre électromagnétaque. Les régions spectrales pour lesquelles l'atmosphère est relativement transparente sont appelées fenêtres. A l'inverse on parle, par abus de langage, de fréquences ou canaux de fréquences opaques lorsque l'atmosphère est opaque pour ces fréquences.
Figure 1 : opacité de l'atmosphère suivant la fréquence.
La figure 1 [Kraus, 1986] résume la situation. Les deux principales fenêtres sont le domaine visible (longueur d'onde comprise entre 0,4 et 0,8 mm) et la fenêtre radio (longueur d'onde comprise entre environ 1 cm et 10 m, soit, en terme de fréquences, entre 30 GHz et 30 MHz). Les rayonnements de longueur d'onde un peu supérieure à 10 m sont réfléchis par l'ionosphère, ce qui permet de réaliser, en ondes courtes, des liaisons radio qui "tournent" autour de la terre. Pour les ondes plus longues, l'ionosphère est absorbante. Pour une autre grande partie du spectre (rayonnements de longueurs d'onde plus courtes que pour la lumière visible) l'atmosphère est opaque.
1.a. L'infrarouge
Pour l'infrarouge, qui s'étend entre les domaines visible et radio, l'opacité de l'atmosphère varie énormément suivant la longueur d'onde. La figure 2 [Harries, 1982] 1 montre le facteur de transmission de l'atmosphère pour les longueurs d'onde supérieures à 4 mm 2. La transmission est bien sûr meilleure à mesure que l'altitude augmente. Les bandes d'absorption principales sont indiquées, sur les courbes données pour une altitude de 4 km, par le nom du composant moléculaire responsable. La figure 3 [Claud, 1989] montre un agrandissement pour la bande 600-800 cm–1 et met en relief la profusion des raies d'absorption et la complexité du domaine infrarouge.
Plus de détails sur cette absorption moléculaire sont donnés dans la partie II, chapitre B.
1.b. Les micro-ondes
La situation est plus simple dans le domaine des micro-ondes (figure 4 [Ulaby et al., 1981]). L'atmosphère est bien transparente pour les fréquences inférieures à 20 GHz. Vers 22 GHz il y a une raie d'absorption peu intense de la vapeur d'eau, puis autour de 60 GHz un complexe de raies de l'oxygène, une raie isolée de l'oxygène encore vers 118 GHz, et une forte raie d'absorption de la vapeur d'eau à 183 GHz. Les régions spectrales entre ces raies constituent des fenêtres pour lesquelles l'atmosphère est de moins en moins transparente à mesure que la fréquence augmente. Au-delà de 300 GHz il existe beaucoup de raies d'absorption, surtout dues à la vapeur d'eau (particulièrement une raie très forte à 557 GHz). On arrive d'ailleurs dans la première région de forte absorption repérée par "H20" (entre 10 et 200 cm–1) sur la figure 2.
Figure 2 : facteur de transmission de l'atmosphère en infrarouge.
Figure 3 : agrandissement d'une partie de la figure 2.
Figure 4 : facteur de transmission de l'atmosphère pour les hyperfréquences.
Désignation des bandes de fréquences
Il est utile ici d'ouvrir une parenthèse sur quelques appellations techniques habituelles. Il existe plusieurs systèmes de désignation, par des lettres, des bandes de fréquence. Ces systèmes utilisent quelquefois les mêmes lettres mais ne sont pas forcément cohérents l'un avec l'autre, en particulier les frontières entre les bandes sont plutôt floues. Les lettres les plus couramment employées sont, dans un ordre approximatif de fréquences croissantes [Ulaby et al., 1981 ; Hughes, 1987 ; Badoual, 1984] (ne parlons pas en plus de la nouvelle désignation reprenant certaines lettres, mais dans l'ordre alphabétique !) :
P, L, D, S, G, C, J, H, X, K, Ku, Kx, Ka,
Q, U, V, E, W, F, D, G 3.
Un système plus régulier et embrassant une plus vaste gamme de fréquences est, en anglais, le suivant : on place entre 300 Hz et 300 GHz successivement les bandes ULF, VLF, LF, MF, HF, VHF, UHF, SHF, EHF 4. Ces bandes sont contiguës et chacune couvre un intervalle dont la fréquence haute est décuple de la fréquence basse 5. La bande EHF est plus communément nommée domaine millimétrique (une longueur d'onde de ce domaine s'exprimant facilement en millimètres).
Au-delà de 300 GHz on entre dans le domaine submillimétrique ou décimillimétrique. La frontière que l'on instaure entre cette région et la région infrarouge est arbitraire et variable. Ce sont plutôt les techniques de réception employées (détection superhétérodyne ou bolomètres) qui distinguent en pratique le submillimétrique de l'infrarouge lointain.
1.c. Influence des nuages et de la pluie
On sait bien que les radiations lumineuses et infrarouges sont arrêtées par une couverture nuageuse, même légère. En revanche, la propagation des micro-ondes, au moins jusque vers 10 GHz, n'est quasiment pas affectée par les nuages ou même par la pluie. Au-dessus de 20 GHz la situation est plus complexe ; l'effet des nuages et de la pluie est d'ailleurs l'objet du chapitre II.C. On peut dire par avance que cet effet augmente rapidement avec la fréquence, la teneur en eau des nuages ou le taux de précipitation ; qu'il est plus sensible (relativement) pour les fréquences des fenêtres ; et qu'enfin et surtout il n'est pas rédhibitoire pour les applications qui seront envisagées au cours des chapitres ultérieurs, dans le cas où la couverture nuageuse n'est pas trop lourde. En revanche, on ne peut pas en dire autant en ce qui concerne le domaine infrarouge, et c'est ce point qui fait l'avantage principal des hyperfréquences sur les ondes infrarouges.
(Notes de bas de page)
1 : Ce genre de figure peut être obtenu par le modèle STRANSAC (voir partie II) du Laboratoire de météorologie dynamique.
2 : En abscisse de ces courbes est porté le nombre d'onde, qui appartient à la terminologie de l'infrarouge ; le nombre d'onde est la grandeur inverse de la longueur d'onde ; l'unité associée est généralement le cm–1 : 1 cm-1 ≈ 30 GHz.
3 : Certaines de ces lettres sont issues de noms de codes utilisés pendant la seconde guerre mondiale.
4 : Les lettres F, V, L, M, H, U, S, E désignent respectivement les mots frequency, very, low, medium, high, ultra, super, ... et extremely !
5 : La bande SHF (3-30 GHz) contient, d'après Badoual [1984], les "ondes centimétriques" ou "hyperfréquences", alors que Robert [1986] appelle hyperfréquence toute fréquence comprise entre 1 et 300 GHz, Larousse [1987] une onde "dont la longueur est de l'ordre du cm", et Mexandeau & Savary [1982] une "radiofréquence suffisamment élevée pour permettre l'emploi de techniques telles que celles des guides d'ondes et des cavités".
2. LE BRUIT
Dans le sens qui lui est donné le plus souvent, la radiométrie est la mesure de l'intensité d'un rayonnement électromagnétique incohérent 1. Un radiomètre mesure l'émission thermique de milieux naturels, et il s'oppose au radar, qui s'intéresse à la réflexion d'un rayonnement qu'il a lui-même envoyé.
En hyperfréquences, beaucoup de termes utilisés reprennent le mot "bruit", qu'on emploie souvent pour radiation, intensité, ou énergie. On va rappeler dans ce chapitre quelques définitions, essentielles pour la suite, concernant le bruit et les températures de bruit ; une présentation plus rigoureuse et détaillée peut se trouver dans Ulaby et al. [1981] ou Kraus [1986].
2.a. Loi de Planck
D'après la loi de la radiation de Planck [1901], un corps noir rayonne uniformément dans toutes les directions avec une luminance spectrale B* donnée par 2 :
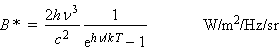 (1)
(1)
h : constante de Planck = 6,6262.10-34 J.s
k : constante de Boltzmann = 1,3806.10-23 J/K
c : vitesse de la lumière dans le vide = 299792458 m/s
T : température, K 3
n : fréquence, Hz.
La luminance spectrale est aussi appelée brillance spectrale, en anglais spectral brightness [Ulaby et al., 1981], quelquefois brightness [Kraus, 1986]. Son intégrale sur toutes les fréquences (unité W/m2/sr) est appelée luminance, intensité spécifique ou brillance énergétique ; en anglais radiance, brightness ou total brightness.
Un matériau qui n'est pas un corps noir a un rayonnement propre qui est forcément moins énergétique. Son émissivité e est le rapport de sa brillance propre à la brillance du corps noir de même température. En toute rigueur, l'émissivité est définie pour une fréquence n et une direction (q, j) bien précisées.
2.b. Approximation de Rayleigh-Jeans et relation entre la puissance et la température
Pour hn << kT (cas des micro-ondes pour des températures terrestres), la loi de Planck se ramène à celle de Rayleigh-Jeans :
![]() (2)
(2)
l : longueur d'onde.
Avec cette approximation, on montre [Ulaby et al., p. 199 ; Kraus, p. 3.39] qu'une antenne sans pertes, observant par tous les "lobes" de son diagramme de rayonnement un corps noir à la température T, reçoit dans la bande de fréquence B (petite par rapport à la fréquence moyenne de réception) la puissance P :
P = kTB (3)
Dans le cas où l'antenne n'observe pas un corps noir, ou alors observe plusieurs sources à des températures différentes, on appelle température radiométrique d'antenne la quantité TA = P/kB, P étant toujours la puissance reçue par l'antenne dans la bande B. La température de brillance d'un corps est la température radiométrique reçue par une antenne sans pertes observant le corps en question dans tous ses lobes (on parle aussi de température apparente de la scène observée).
Le résultat résumé par la relation (3) est à rapprocher de la formule donnée par Nyquist [1928] pour la puissance de bruit W disponible dans une bande B, aux bornes d'une charge adaptée, à la température T :
W = kTB (4)
Les relations (3) et (4), exprimant une linéarité entre puissances et températures, sont le fondement de l'utilisation de la température de bruit comme mesure de l'énergie reçue par une antenne, ou mesure du bruit fourni ou ajouté par un composant quelconque dans une ligne de transmission.
La relation de Rayleigh-Jeans, support de la linéarité de la relation puissance-température, devient osée pour des fréquences supérieures à 100 GHz et des températures très basses (hn ≈ kT pour n = 200 GHz et T = 10 K). Ainsi, pour le rayonnement cosmique à environ 3 K, la correction à apporter pour conserver une relation virtuelle puissance-température toujours linéaire est présentée au chapitre II.A.
2.c. Bruit d'une chaîne de réception
Rappelons la définition de la température additionnelle de bruit d'un quadripôle [Darricau, 1973] : un quadripôle réel de gain G (ou d'atténuation L = 1/G) est équivalent à un quadripôle parfait (non bruité) soumis à son entrée à une source additionnelle de bruit :
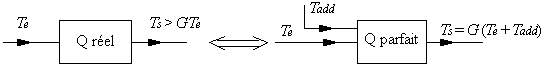
Te, Ts : températures équivalentes de bruit à l'entrée et à la sortie du quadripôle (Te = Pe /kB ; Ts = Ps /kB)
Tadd : température additionnelle de bruit.
La température additionnelle de bruit d'un atténuateur d'affaiblissement L et de température physique ("réelle") T0 est (L – 1) T0.
La température équivalente de bruit TR d'un récepteur est définie comme la température additionnelle de bruit de toute la chaîne de réception, constituée successivement des quadripôles Q1, Q2, ..., Qn :
![]() (5)
(5)
(On parle alors de température de bruit ramenée à l'entrée du récepteur.)
Par exemple, pour un récepteur simplifié comprenant un mélangeur d'affaiblissement de conversion LM et de température de bruit TM 4,, suivi d'un amplificateur à fréquence intermédiaire (FI) de température de bruit TFI, on a : TR = TM + LM TFI.
Depuis 1952 et la définition adoptée par l'IRE (Institute of Radio Engineers), le facteur de bruit est [Mumford & Scheibe, 1967] :
![]() (6)
(6)
Il est bon de remarquer que, dans le cas où une chaîne de réception ne comporte que des éléments passifs à la température T0 = 290 K, avec éventuellement un mélangeur pour lequel le facteur de bruit égale l'affaiblissement de conversion, et un amplificateur seulement comme dernier élément de la chaîne, on peut sommer les atténuations apportées par les éléments passifs et par le mélangeur, et le facteur de bruit de l'amplificateur, exprimés en dB, pour obtenir le facteur de bruit de l'ensemble de la chaîne.
2.d. Sensibilité radiométrique
La sensibilité (on dit aussi résolution) radiométrique DT est le plus petit changement dans la température d'antenne TA qui peut être détecté à la sortie du récepteur. En d'autres termes, DT est l'écart-type de la fluctuation aléatoire de la température de bruit mesurée à la sortie du système.
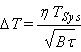 (7)
(7)
TSys : température de bruit du système, somme des température d'antenne et température de bruit du récepteur
B : largeur de bande équivalente avant détection
t : temps d'intégration (temps d'observation, voir III.A.2)
h : facteur — supérieur ou égal à 1 — dépendant du type de radiomètre utilisé.
L'expression (7) [Tiuri, 1964 ; Kraus, 1986 ; Evans & McLeish, 1977, pour une démonstration un peu différente] est valable pour un récepteur sans dérive de gain. Nous reviendrons dans la partie III sur la définition exacte de B et t, les subtilités pour TSys et la valeur du facteur h. Il faut pour l'instant savoir que (7) est une équation fondamentale pour la radiométrie. En effet elle indique que la sensibilité (donc la connaissance relative de la grandeur radiométrique mesurée) est tributaire :
– De la température de bruit du récepteur : celle-ci doit être la plus basse possible ;
– Du temps d'intégration : il doit être le plus grand possible ;
– De la largeur de bande du système : elle doit être la plus grande possible, dans la limite des contraintes de résolution spectrale et de température de bruit du récepteur (un amplificateur large bande par exemple étant plus bruyant qu'un amplificateur faible bande).
La sensibilité radiométrique n'est pas le seul critère de qualité d'un radiomètre. Sont abordées plus loin (chapitre III.C) les notions de précision absolue, précision de l'étalonnage, etc.
(Notes de bas de page)
1 : Ce qui n'empêche pas d'employer des techniques de réception cohérente.
2 : Les notations du type hn / kT doivent être lues selon hn / (kT). Les notations concernant les unités suivront le modèle : W/m2/Hz/sr est équivalent à W.m–2.Hz–1.sr–1.
3 : En 1967, à la Conférence internationale sur les poids et mesures, le degré Kelvin a cédé la place, en tant qu'unité de température, au kelvin (symbole K) [Ulaby et al., 1981, p. 193].
4 : Pour les questions de bande simple ou double, voir la partie III.
Sommaire Précédent Suivant Accueil



