D. EMISSION ET REFLEXION A LA SURFACE

Résumé — Après quelques généralités sur la réflexion des ondes millimétriques sur différences surfaces, nous présentons un modèle de réflexion sur la mer, adapté de celui de Wilheit [1979] : il s'agit d'un modèle géométrique, prenant en compte une réflexion spéculaire sur des facettes planes élémentaires dont la distribution de probabilité des pentes est supposée connue [Cox & Munk, 1954]. Nous évaluons ensuite l'influence de la réflexion du soleil suivant la rugosité de la mer.

1. GENERALITES

Il y a beaucoup de références dans la littérature sur la modélisation des propriétés émissives de la surface terrestre, suivant la fréquence et la nature du sol. Nous n'allons pas rappeler tous ces modèles, bien décrits par exemple par Ulaby et al. [1981, 1982 et 1986].

Un cas simple est celui d'une surface lisse. Par surface "lisse", on entend une surface dont l'écart type des irrégularités (par rapport à un plan) est petit devant la longueur d'onde. On se place alors dans le cadre de l'optique géométrique. La réflexion d'un rayonnement incident est alors spéculaire (suit les lois de Snell-Descartes). Le facteur de réflexion est donné par les formules de Fresnel, soit, dans le cas le plus général [Ulaby et al., 1981, p. 230] :

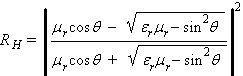
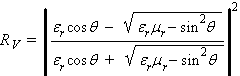(1)

R_H, R_V : facteurs de réflexion (pour l'énergie) pour les polarisations horizontale et verticale

e_r, m_r : permittivité et perméabilité magnétique, relatives, du milieu sur lequel s'exerce la réflexion par rapport au milieu du rayonnement incident (e_r m_r = n², n étant l'indice de réfraction)

q : angle d'incidence (angle, compris entre 0 et p/2, entre la normale à la surface et la direction de propagation de l'onde incidente).

Plutôt que de polarisations horizontale et verticale, il serait mieux dans ce cas de parler de polarisations orthogonale et parallèle (respectivement). Rappelons que ces deux derniers termes qualifient la direction du champ électrique relativement au plan d'incidence défini par la direction de propagation et la normale à la surface. Pour une surface "horizontale" telle que la surface de la terre, la direction du champ électrique en polarisation horizontale est effectivement horizontale, mais celle du champ en polarisation verticale n'est pas verticale puisqu'elle fait un angle p/2 – q avec la verticale. Si q est nul, il y a "confusion" des deux polarisations.

L'émissivité de la surface, pour une polarisation, est le complément à 1 du facteur de réflexion correspondant. La température apparente de la surface (température montante) s'écrit alors en fonction de la température apparente descendante et de la température du sol (R étant différent pour chaque polarisation) :

T = R T_¯ + (1 – R) T_sol (2)

On supposera toujours que le rayonnement descendant n'est pas polarisé.

Dans le cas où m_r = 1 et e_r est réel (milieux sans pertes), R_V (ou R_// ) s'annule pour l'angle de Brewster q_B :

(3)

Si e_r est complexe, R_V passe par un minimum non nul pour un "pseudo-angle de Brewster" [Ohman, 1977].

A l'autre extrême, il y a le cas d'une surface très rugueuse, c'est-à-dire dont les irrégularités sont comparables ou grandes devant la longueur d'onde du rayonnement incident. On choisit alors souvent de supposer que la surface émet une brillance indépendante de la direction q : c'est la loi de Lambert [Renault, 1980]. Il reste encore à déterminer l'émissivité.

Nous nous sommes surtout intéressés à la modélisation de l'émission et de la réflexion à la surface de la mer. Mais nous allons d'abord dire quelques mots sur les autres types de surface.

La connaissance de l'émissivité est liée à celle de la permittivité e_r du milieu réfléchissant. Le milieu observé est souvent une juxtaposition de milieux bien différents : ville, champs, lac, etc. Ces différences, en températures de brillances, sont d'ailleurs bien visibles sur les jolies images à 7 m de résolution présentées par Wilson et al. [1986], obtenues à 98 GHz depuis un hélicoptère à 750 m d'altitude.

Pour un modèle destiné à un satellite dont la limite de résolution au sol est de l'ordre de plusieurs kilomètres, on est bien obligé de se contenter d'une émissivité moyenne, typique. Sa valeur pour des fréquences millimétriques est proche de 1, et d'autant plus grande que l'humidité du sol est basse (le degré d'humidité est l'élément essentiel gouvernant la valeur de la permittivité des terrains). Phalippou et al. [1989] ont utilisé des indices de végétation. Pour l'émissivité des simulations ITRA [Chédin et al., 1988 (b)], on a choisi 0,95.

Des mesures par avion [Hollinger et al., 1984] ont montré que l'émissivité de la glace pour des fréquences supérieures à 90 GHz varie de 0,6 à 1 suivant le type de glace (la glace plus ancienne est plus réfléchissante).

L'émissivité de la neige est elle aussi très variable, en fonction de sa qualité, et plus précisément de son contenu en eau libre. Pour la neige sèche, la profondeur de pénétration d'un rayonnement incident est grande : 2 m à 37 GHz par exemple. Les propriétés de la surface sous-jacente interviennent alors beaucoup dans l'émissivité globale. Pour la neige fondue, on est très proche d'un corps noir. Voir la note de synthèse de Phulpin & Le Borgne [1984] et encore et toujours Ulaby et al. [1982 et 1986].

2. NOTRE MODELE POUR LA MER

2.a. Introduction

Comparée à la terre, la mer a des caractéristiques moins changeantes dans l'espace : l'état (calme ou agité), la température, la salinité sont des paramètres qui restent généralement stables sur d'assez grandes distances, du moins loin des côtes. Cette homogénéité permet de concevoir des modèles d'émissivité assez "propres".

Pour les fréquences qui nous intéressent, le paramètre essentiel gouvernant l'émissivité et la température apparente est le vent, par les vagues et les vaguelettes qu'il crée et qui déterminent la "rugosité" de la mer (la figure I.B.-1 montrait l'influence des autres paramètres suivant la fréquence). Encore faut-il savoir de quel vent il s'agit. La houle qui agite la mer peut être due à un vent ayant soufflé la veille, et qui n'a plus rien de commun, ni en force, ni en direction avec le vent présent. On supposera dans ce qui suit qu'un régime permanent est établi, c'est-à-dire que l'état de la mer est uniquement déterminé par le vent du moment.

Modèle de distribution de pentes

Une façon de décrire l'état de la mer est de donner la distribution des pentes à la surface des vagues. Cox & Munk [1954] ont analysé des photographies aériennes de l'image réfléchie du soleil, pour des vents de 0 à 14 m/s. Résultant de cette analyse, la densité de probabilité à deux dimensions des paramètres définissant les pentes suit quasiment une loi de Gauss. De façon imagée, on peut voir la probabilité d'une pente comme le quotient de la surface de toutes les facettes élémentaires ayant cette pente, par la surface totale observée.

Les paramètres z_u et z_c définissant une pente sont reliés aux angles d'azimut a et de site b de la pente. L'azimut est mesuré par rapport au vent : a = 0 pour une pente dont la normale est dans le même plan que la verticale et la direction du vent ; b est l'angle (positif) que fait la normale à la pente avec la verticale (les notations sont un peu différentes chez Cox & Munk) :

z_u = cosa tgb (4)

z_c = sina tgb (5)

Les variances dans les deux directions principales sont reliés à la vitesse du vent W (en m/s, mesurée à 41 pieds au-dessus de la mer) de façon linéaire :

(6)

(7)

L'indice u (upwind) désigne la direction du vent (le plan défini par la normale à la pente et la verticale contient la direction du vent), et l'indice c (crosswind) la direction horizontale orthogonale.

La densité de probabilité des paramètres des pentes s'écrit :

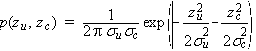(8)

En fait, des corrections mineures par rapport à une distribution parfaitement gaussienne sont prises en compte (coefficients de "skewness" et "peakedness") pour donner une distribution de Gram-Charlier.

Pour d'autres types de mesures donnant d'autres distributions de pentes, et pour des analyses et comparaisons critiques avec les conclusions de Cox & Munk, voir par exemple Schooley [1961], Tang & Shemdin [1983] et Hwang & Shemdin [1988].

Différentes approches

On trouve dans la littérature plusieurs approches pour calculer l'émissivité de la mer.

Stogryn [1967] calcule l'émissivité à partir des coefficients de diffusion proposés par Peake [1959], qui représentent, en gros, la part d'énergie diffusée d'une direction vers une autre. Dans "l'approximation de Kirchhoff" et dans certains cas de surfaces très rugueuses, ces coefficients de diffusion sont donnés par une expression plutôt compliquée, avec dépendance suivant les variances de la distribution des pentes (Cox & Munk par exemple). Hollinger [1971] mesure la température apparente de la mer depuis une tour, vers 1, 8 et 19 GHz. La comparaison avec la théorie de Stogryn n'est pas trop mauvaise, mais est bien meilleure si l'on multiplie les écarts types avancés par Cox & Munk par 1/3, 1/2 et 2/3, respectivement pour les trois fréquences.

Wu & Fung [1972], Wentz [1975] et plus récemment Guissard & Sobieski [1987] raisonnent sur deux échelles : ils superposent la contribution des grandes ondulations de la surface à celle des petites irrégularités (les vaguelettes). Ces modèles sont d'autant plus efficaces par rapport à celui de Stogryn que la fréquence est basse.

Après ces modèles abstrus, Wilheit [1979 (a et b)] présente un modèle "géométrique", qu'il dit similaire à celui de Stogryn mais qui est beaucoup plus simple dans sa formulation. Notre modèle [Prigent & Abba, 1990] est inspiré de celui de Wilheit, mais nous menons le calcul de façon rigoureuse plus longtemps¹.

(Note de bas de page)

1 : Warner [1986], en reprenant la formulation de Wilheit, avait peut-être apporté les mêmes modifications que nous ; nous n'avons pas pu vérifier, n'ayant qu'un extrait de la référence citée.

2.b. Description générale

La mer est représentée comme un ensemble de facettes planes, dont la distribution des pentes est donnée par Cox & Munk. Chacune des facettes est supposée grande devant la longueur d'onde d'observation et un rayonnement incident est donc réfléchi de façon spéculaire. Le facteur de réflexion, pour chaque facette et chaque polarisation, est donné par les relations (1). On est donc placé dans l'approximation de l'optique géométrique.

Wilheit prend alors pour facteur de réflexion de toute la surface marine la moyenne pondérée des facteurs de réflexion de toutes les facettes élémentaires. Pour chaque facette, le coefficient de pondération est la probabilité de présence de la facette. Avec ce facteur de réflexion fictif il applique la relation (2). En toute rigueur cette façon de procéder est bâtarde et ne se justifie qu'en vue d'une économie de temps de calcul. En effet, les facettes étant orientées dans des directions différentes, les rayonnements descendants renvoyés vers le radiomètre proviennent de directions différentes, et ont donc des températures différentes (ces températures dépendent de l'angle zénithal du rayonnement descendant). Il n'y a donc pas à proprement parler une température descendante, mais autant de températures descendantes que de pentes différentes, ou plutôt d'angles b différents (figure 1, facettes 1 et 2).

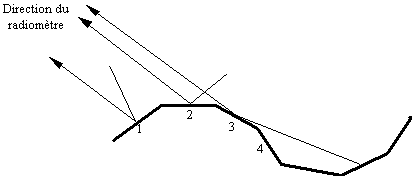
Figure 1 : ensemble de facettes modélisant la surface de la mer.

Dans notre modèle nous appliquons donc la relation (2) à chaque facette. L'angle q des relations (1) est l'angle que fait la normale à la facette avec la direction de visée du radiomètre et aussi l'angle entre la normale et la direction d'arrivée du rayonnement descendant à considérer.

Enfin les contributions élémentaires sont sommées, en les pondérant par la distribution des pentes.

2.c. Remarques et détails

Les détails des calculs géométriques sont présentés par Prigent-Benoit [1988]. Quelques remarques complémentaires sont ici rappelées ou rajoutées.

– La constante diélectrique de l'eau est calculée, en fonction de la fréquence, de la température et de la salinité, avec les formules de Klein & Swift [1977].

– Chaque facette est traitée en polarisation parallèle et orthogonale (relations (1)). Les températures de brillance dans ces deux directions, à la "sortie" de la facette, sont ensuite transformées en températures en polarisations horizontale et verticale, ces deux termes devant être compris relativement à la surface marine globale et au radiomètre.

– Nous tenons compte de la direction de visée du radiomètre par rapport à la direction du vent : la distribution de pentes n'a pas le même écart type dans les directions upwind et crosswind. Wilheit se contente d'une distribution non directionnelle, en prenant pour variance la somme des variances dans les deux directions (voir Cox & Munk pour la définition des distributions mono- et bi-directionnelles).

– Les facettes cachées (facette 4 sur la figure 1) ne sont pas prises en compte dans le calcul. Ces facettes n'apparaissent que pour des visées éloignées du nadir et pour des vents forts. On élimine ainsi certaines des facettes plus pentues que l'angle de visée, si l'on peut dire, mais pas les facettes moins pentues qui sont cachées par d'autres : ce serait le cas de la partie gauche de la facette à droite de la facette 4, sur la figure 1. C'est un défaut du modèle qui n'est pas corrigible.

– Certaines facettes (facette 3 sur la figure 1) sont orientées de telle façon que le rayonnement "descendant" incident à considérer provient en fait de sous l'horizon. Dans ce cas, quelle est la température incidente ? Deux simplifications sont possibles. La première est de supposer qu'il y a une double réflexion : Warner [1986] élève au carré le facteur de réflexion. Mais on ne connaît toujours pas la direction du rayonnement descendant concerné, car la pente responsable de l'autre réflexion a évidemment une orientation inconnue par rapport à la pente suivante. La deuxième solution, que Wilheit et nous avons choisie, est de prendre, pour température incidente, tout simplement la température de la mer : cette simplification revient à supposer que le rayon a subi des réflexions multiples (en fait en grand nombre) avant d'aboutir sur la pente finale.

– Dans les modèles de diffusion (non géométriques), on mentionne souvent le problème de la "conservation de l'énergie", qui apparaît lorsque l'on simule mal les facettes cachées et les diffusions multiples. Pour notre modèle, le fait de prendre la température de la mer comme température incidente en cas de multiples réflexions surestime légèrement la température apparente montante.

– La contribution de chaque facette doit, avant sommation, être multipliée par le cosinus de l'angle d'incidence q sur la pente : c'est la contribution projetée de la facette dans la direction du radiomètre qui doit être considérée.

– C'est la densité de probabilité des pentes vues au nadir que Cox & Munk ont définie, d'où dans leur article [1954, p. 844] l'apparition du secb, b étant l'angle de site d'une pente. Pour nous, la contribution de chaque facette est à multiplier par secb, puisque c'est la surface réelle de la facette, et non la surface projetée horizontalement, qui nous intéresse.

– C'est évidemment un nombre fini de pentes différentes que l'on considère dans le calcul. On commence par échantillonner de façon régulière les deux paramètres z_u et z_c caractéristiques des pentes. En arrêtant le balayage à –2,5s et à +2,5s, on encadre 97,5 % des pentes possibles (voir les tables de la fonction de répartition d'une loi normale). Après la sommation de toutes les contributions, on divise le résultat par la somme des facteurs pondérateurs des températures élémentaires.

– La température descendante devrait être calculée pour chaque pente. Vu le nombre élevé de pentes à considérer (voir plus loin), on se contente de calculer la température descendante pour quelques angles zénithaux (moins de 25) et d'interpoler de façon linéaire, entre deux températures calculées, pour l'angle voulu.

– Ce modèle géométrique est d'autant plus valable que la fréquence est élevée. D'après Wilheit [1979 (a)], une partie seulement des pentes mesurées par Cox & Munk (à des longueurs d'onde dans le visible) a un effet à basse fréquence ; les plus petites vaguelettes, qui sont responsables des plus fortes pentes, ne sont pas "vues" par des ondes dont la longueur est de l'ordre de la dizaine de centimètres. C'est la justification théorique des facteurs correctifs 1/3, 1/2 et 2/3 mentionnés précédemment pour les fréquences inférieures à 30 GHz. Au-delà de 35 GHz et probablement jusqu'aux fréquences du domaine visible, Wilheit pense que toutes les pentes mesurées par Cox & Munk sont "actives".

2.d. L'écume

De nombreux modèles d'émissivité de l'écume ont été imaginés pour les ondes centimétriques. Au-delà de 50 GHz, l'écume semble se comporter comme un corps noir (émissivité = 1). Voir en particulier les figures 9 et 10 de Wilheit [1979 (b)].

Le taux de couverture d'écume est fonction du vent. Nous avons adopté la relation proposée par Wu [1979]. La fraction F de la surface recouverte d'écume est, pour un vent W exprimé en m/s et mesuré à 10 m de hauteur :

F = 1,7 10^–6 W^3,75 (9)

A noter que la relation indiquée par Wilheit [1979 (b)] est différente :

F = 0,006 (W – 7) pour W > 7 m/s

F = 0 pour W < 7 m/s (10)

Pour chaque facette, les températures apparentes en polarisations parallèle et orthogonale sont alors modifiées de la façon suivante :

T ' = (1 – F) T + F T_mer (11)

2.e. Définition de l'émissivité

Contrairement à Wilheit, nous ne pouvons pas définir réellement l'émissivité, du moins pas dans le sens de la relation (2) avec e = 1 – R. En effet nous avons vu qu'il n'y avait pas de température descendante à proprement parler. Nous pourrions cependant choisir de définir l'émissivité par référence à une réflexion spéculaire (e variant aussi avec q) :

T(q) = e T_mer + (1 – e)T_¯(q) (12)

Curieusement, dans certains cas, cette définition conduit à une émissivité négative. Ces cas sont ceux où q est élevé (incidence rasante), et où le vent est assez fort pour que les facettes les plus "actives" soient celles qui renvoient des températures provenant de directions pas trop éloignées du zénith, donc assez faibles ; en conséquence, la température montante peut être inférieure à la température descendante dans la direction spéculaire, d'où l'émissivité négative obtenue en résolvant (12).

La deuxième possibilité est de définir l'émissivité comme le facteur multiplicatif de la température de la mer dans l'expression de la température montante. Cela revient à annuler toutes les températures descendantes (atmosphère parfaitement transparente et rayonnement cosmologique négligé) et à faire le rapport de la température montante et de la température de la mer. Cette définition, qui est adoptée pour la suite, est finalement la même que celle de Wilheit et nous amène à écrire :

T = e T_mer + (1 – e)T_ß (13)

T_ß est une somme pondérée de températures descendantes. e est indépendant de ces températures.

2.f. Résultats

Le nombre de pentes élémentaires qu'il faut simuler pour obtenir une représentation correcte de la distribution de probabilité dépend beaucoup de la force du vent et de l'angle d'incidence. En général à partir de 100, et plus rarement à partir de 1000 pentes, on ne constate plus d'amélioration si l'on augmente le nombre de pentes. Une centaine de pentes correspond à 5 valeurs positives et 5 valeurs négatives possibles pour chacun des paramètres z_u et z_c.

Les fréquences qui nous intéressent pour les simulations sont surtout les fréquences des canaux fenêtres, et en particulier 89 et 157 GHz pour la préparation des vols de MARSS.

La figure 2 (légende en anglais, ainsi que les suivantes) montre la température apparente de la mer à 157 GHz, pour différentes vitesses de vent. Lorsque le vent est nul on est presque dans les conditions de la réflexion spéculaire, la seule différence venant de la distribution des pentes qui n'est pas tout à fait nulle pour la direction orthogonale au vent, d'après la relation (6). 7 m/s correspond à un vent de force 4, et 14 m/s à un vent de force 6 à 7. L'atmosphère supposée est U.S. Standard, la température de surface est 287,35 K et la salinité 36 ‰ (i.e. 36 g de sel pour 1000 g d'eau).

L'effet du vent est important, surtout en polarisation horizontale. En polarisation verticale, l'effet est nul pour des angles d'incidence proches de 45°. A 89 GHz, c'est plutôt vers 50° que cette invariance apparaît. Cette particularité bien connue de la température apparente a été l'une des raisons du choix d'un angle de sondage d'environ 50° pour plusieurs radiomètres à balayage conique.

Agrandir

Figure 2 : température apparente de la mer à 157 GHz.

La figure 3 montre l'émissivité calculée toujours à 157 GHz. L'influence du vent y est beaucoup moins sensible que sur la figure 2. D'autre part les figures 2 et 3 indiquent que l'on ne peut pas négliger l'influence de l'écume pour un vent assez fort (à 14 m/s, F = 0,034), d'où l'importance d'utiliser une expression correcte pour le taux de couverture d'écume.

Pour les simulations amenant les figures 2 et 3, nous avons supposé que la projection de la direction d'observation sur le plan horizontal était identique à la direction du vent. La figure 4 indique la différence dans la température de brillance entre une telle observation et une observation dont la projection est dans la direction orthogonale (90°), ou dans la même direction mais dans l'autre sens (180°). Dans ce dernier cas la différence est due à l'asymétrie de la distribution des pentes suivant leur orientation face au vent ou dos au vent.

En fait les différences sont petites, toujours inférieures à 2 K, ce qui justifie la simplification opérée par Wilheit qui utilise une distribution non directionnelle.

Agrandir

Figure 3 : émissivité de la mer à 157 GHz .

Agrandir

Figure 4 : différence dans la température de brillance suivant la direction du vent.

Enfin un dernier point concerne une tentative de simplification du calcul, pour faciliter une éventuelle étape d'inversion et répondre à une suggestion de D. Pick du British Meteorological Office. On peut récrire (13) ainsi :

T(q) = e(q) T_mer + [1 – e(q)] T_¯(x) (14)

Dans cette expression, T_¯(x) est la température descendante dans la direction x, et n'est plus une somme pondérée de températures descendantes. Existe-t-il une relation simple (en fonction du vent) entre q et x ?

L'ensemble des simulations que nous avons passées ne nous a pas permis d'en trouver une. Tout d'abord, si l'on fait x = q comme Wilheit, on commet par rapport à notre modèle une erreur sur T(q) qui peut être assez forte : plus de 5 K à 157 GHz pour W = 14 m/s et q = 45°. Pour obtenir la température montante correcte, par exemple à 157 GHz et pour W = 7 m/s, il faut x = 20°, 26°, 37°, 50° et 62° respectivement pour q = 0°, 15°, 30°, 45° et 60°. Ces valeurs de x sont différentes pour des fréquences ou des vents différents. Tous ces chiffres concernent la polarisation horizontale ; les différences entre q et x et suivant les conditions sont plus faibles en polarisation verticale.

Ces réflexions sont à rapprocher des considérations de Wentz [1983], reprises par Guissard & Sobieski [1987]. Ces auteurs écrivent (nous reprenons nos notations précédentes) :

T_ß = T_¯(q) (1 + d) (15)

d est appelé "correction de diffusion" ; il vaut 0 pour une réflexion spéculaire et est plus fort pour la polarisation horizontale. Guissard & Sobieski ont montré que ce terme dépend (entre autres) de la vitesse du vent de façon fortement non linéaire, et de l'opacité atmosphérique. En définitive il n'est pas simple du tout de simplifier un modèle d'émissivité de la mer !

Enfin signalons qu'il est difficile de comparer notre modèle à des mesures, car les résultats expérimentaux bien exposés sont rares. Les mesures de Hollinger [1971] se rapportent à des fréquences trop basses pour notre modèle. Là encore nous attendons avec impatience les vols opérationnels de MARSS. A ce sujet, signalons que notre modèle, conçu pour un radiomètre visant dans une seule direction, devra être adapté pour intégrer l'effet du diagramme de rayonnement réel de l'instrument : pour MARSS, le lobe à 3 dB fait 10°.

3. REFLEXION DU SOLEIL

Pour l'instant, la température descendante que nous avons considérée a été constituée par le rayonnement de l'atmosphère et le fond cosmique. Cependant dans certains cas de figure, il faut tenir compte du soleil. Dans cette section nous envisageons les cas où la réflexion du soleil sur la surface marine intervient de façon plus ou moins sensible dans le transfert radiatif.

3.a. Hypothèses de calcul

Dans le domaine millimétrique, la température apparente du Soleil est la même que dans les domaines infrarouge et optique : environ 6000 K ; son diamètre angulaire est b_* = 0,534°, et son angle solide W_* = 2p (1 – cosb_*/2) = 6,82 10^–5 sr. Ce n'est qu'à partir des longueurs d'onde centimétriques que le diamètre apparent du Soleil augmente et que son comportement s'éloigne sensiblement de celui d'un corps noir, pour atteindre, pour les ondes métriques, des températures apparentes de l'ordre de plusieurs milliards de kelvins en période d'activité maximale [Kraus, 1986].

A 89 GHz, fréquence la plus "transparente" parmi celles qui nous occupent, l'absorption atmosphérique est typiquement 1,45 dB, et donc la température apparente du Soleil au niveau du sol n'est plus que T_* = 4300 K. Le facteur de réflexion R de la surface marine pour des angles d'incidence pas trop grands est voisin de 0,4.

Nous supposerons que l'antenne du radiomètre a un diagramme de rayonnement très simple, constitué d'un seul lobe de diamètre angulaire b_A et d'angle solide W_A ≈ b_A² [Ulaby et al., 1981, p. 102]. Nous supposerons en outre que le gain de l'antenne est constant sur tout le lobe. Nous prendrons trois exemples :

– Météosat : b_A = 0,08°,

– AMSU-B : b_A = 1,1°,

– MARSS : b_A = 10°.

3.b. Cas d'une surface plane

Si l'antenne ne pointe pas dans la direction de l'image du soleil sur la mer, il n'y a évidemment aucun effet du soleil. Sinon, il faut distinguer deux cas.

W_* > W_A

C'est le cas de Météosat. Dans la pire situation, tout le lobe de l'antenne "regarde" le soleil. L'augmentation de température apparente T_AP* due au soleil est alors :

T_AP* = R T_* = 1720 K (16)

W_* < W_A

Dans le pire des cas, le lobe de l'antenne voit la totalité du soleil (figure 5).

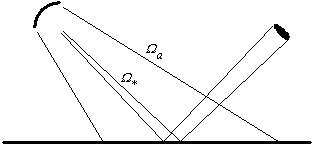
Figure 5 : réflexion spéculaire du soleil.

T_AP* = R T_* W_*/W_A (17)

Soit 320 K pour AMSU-B, et 3,9 K pour MARSS.

3.c. Cas d'une surface agitée (notre modèle)

Pour simplifier nous prendrons la distribution de pentes de Cox & Munk omnidirectionnelle :

(18)

s² = s_c² + s_u² (19)

[ En posant z_u² + z_c² = tg²b = r², on vérifie que :

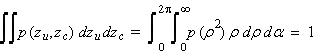(20) ]

La distribution de pentes est centrée sur les pentes horizontales. Le cas le plus gênant (et surtout le plus simple à traiter), que nous allons maintenant considérer, se produit donc lorsque le soleil est dans la direction de réflexion spéculaire, d'angle zénithal q ¹.

W_* >> W_A (Météosat)

Un rayon descendant qui, par réflexion sur une certaine facette, est renvoyé dans la direction de l'antenne, provient du Soleil si l'angle qu'il fait avec la direction du centre du Soleil (à savoir la direction spéculaire) est inférieur à b_*/2. Par quelques calculs de géométrie vectorielle, et en faisant l'approximation b_* << 1, on montre que l'angle solide dans lequel sont dirigées les normales aux facettes qui apparaissent, pour l'antenne, illuminées par le soleil, peut être vu comme un cône de base elliptique dont les demi-axes "angulaires" sont b_*/4 et b_*/(4cosq). Pour calculer la température apparente due au soleil, il faudrait alors intégrer les contributions de toutes les pentes dont la normale est intérieure à ce cône. Un calcul simple n'est possible que pour un cône à base circulaire ; la température apparente qui est calculée ci-dessous est donc une majoration de la température réelle. Dans ce calcul, tous les angles b sont assimilés à leur tangente, et l'angle q supposé "raisonnable" :

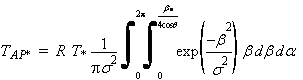(21)

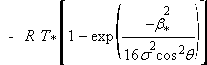(22) [Note : - = ≈]

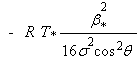(23) [Note : - = ≈]

La dernière approximation est valable si la mer est assez rugueuse (s assez grand).

W_* << W_A (MARSS)

Le raisonnement est le même que pour W_* >> W_A, sauf que les normales des pentes concernées par la réflexion du soleil sont maintenant à chercher dans un cône défini par b_A au lieu de b_*. Comme pour le cas d'une surface plane, il faut multiplier par W_*/W_A ≈ b_*²/b_A². En définitive, on retrouve exactement la relation (23).

Nous supposerons que dans le cas intermédiaire où W_* est de l'ordre de W_A (AMSU-B), la relation (23) est toujours valable.

Nous avons donc, pour les trois projets, et pour un angle de sondage q de 45° :

– W = 2,5 m/s (mer calme), s ² = 0,016 : T_AP* = 1,2 K,

– W = 14 m/s (mer agitée), s ² = 0,075 : T_AP* = 0,25 K.

Il est facile de lancer des simulations sur le modèle programmé, en traitant correctement les pentes touchées par la réflexion du soleil parmi toutes les pentes calculées (il faut évidemment simuler un très grand nombre de pentes). Les résultats, légèrement inférieurs aux valeurs données ci-dessus qui découlaient d'une surestimation, confirment que l'influence du soleil peut être négligée pour une mer pas trop calme, et cela quel que soit le pouvoir de résolution spatiale du radiomètre. En revanche nous avons vu que dans le cas d'une mer très calme et d'une réflexion spéculaire, le soleil pouvait être très gênant pour Météosat et AMSU-B. Cependant, pour Météosat, ce problème ne peut évidemment survenir qu'entre les tropiques, et jamais sur l'Europe.

(Note de bas de page)

1 : Ce n'est peut-être pas tout à fait vrai : il faudrait en toute rigueur tenir compte des angles de projection q et b dont le rôle a été précisé auparavant (2.c).

Sommaire Précédent Suivant Accueil