C. ABSORPTION ET DIFFUSION
PAR LES NUAGES ET LES PRECIPITATIONS

Résumé — Nous présentons l'équation de transfert radiatif dans un milieu diffusant, ce qui conduit à définir la température radiométrique diffusée, la fonction de phase, et les coefficients d'absorption et de diffusion qui sont calculés à partir des facteurs d'efficacité de Mie ou de Rayleigh et d'une distribution de tailles de gouttes. Après avoir parlé des problèmes variés rencontrés au cours de la modélisation, nous comparons les effets d'un nuage et d'une pluie raisonnables pour des fréquences proches de 55 et 118 GHz.

Nous allons traiter succinctement les questions relatives à la façon dont nous avons modélisé l'absorption et la diffusion par les nuages et les précipitations. C. Prigent-Benoit [1988] a déjà exposé en détail les principaux aspects de cette modélisation. Par souci de cohésion avec les autres chapitres, nous allons rappeler les idées fondamentales (la plupart des résultats essentiels seront donnés sans démonstration), et les références majeures.

1. EQUATION DE TRANSFERT DANS UN MILIEU DIFFUSANT

Dans un milieu où l'on ne néglige plus la diffusion, l'équation (11) à laquelle nous étions parvenus au chapitre A devient maintenant [Ulaby et al., 1981, p. 216] :

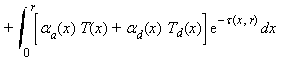(1)

a_a est le coefficient d'absorption du milieu et a_d est le coefficient de diffusion. La somme de ces deux coefficients est le coefficient d'atténuation ou d'extinction a, qui est toujours la dérivée de l'épaisseur optique t. T_d est appelée température radiométrique diffusée ; avec des notations vectorielles qui étaient implicites jusqu'à présent :

(2)

T_d apparaît comme l'intégration sur tous les angles solides des températures apparentes issues de toutes les directions de l'espace, pondérées par la fonction y, appelée fonction de phase, ou encore indicatrice de diffusion. y(, ) représente la part d'énergie diffusée de la direction vers la direction .

2. APPLICATION A L'ATMOSPHERE STRATIFIEE

Comme pour une atmosphère sans diffusion, nous intégrons l'équation (1) pour une couche, en supposant que tout est constant sur cette couche :

(3)

l'expression suivante a le même développement limité que (3) jusqu'au deuxième ordre en t (t_a et t_d ont les mêmes définitions par rapport à a_a et a_d que t par rapport à a) :

(4)

Cette expression est plus aisément interprétable que la précédente : les effets de l'absorption et de la diffusion sont séparés ; l'émission due à l'absorption (les deux premiers facteurs du deuxième terme du second membre) subit une atténuation due à la diffusion par, en moyenne, une demi-couche, d'où le facteur e^–td/2 ; et réciproquement pour le troisième terme.

On ne peut pas appliquer (3) de couche en couche aussi simplement que pour une atmosphère sans diffusion. Dans l'expression de la température diffusée intervient la température apparente que l'on cherche à calculer. Il faut procéder par itération jusqu'à obtenir une convergence espérée, comme l'ont fait Wilheit et al. [1977] qui nous ont inspirés, ou d'autres avant eux. La première fois sont calculées les températures de brillance montantes et descendantes dans quelques directions et pour toutes les couches, sans tenir compte de la diffusion. Puis, pour les étapes suivantes, on calcule les températures diffusées à partir des températures de brillances qui ont été calculées à l'étape précédente ; pour ce calcul on transforme (2) en somme discrète sur les "quelques" directions mentionnées plus haut. En général, quatre ou cinq étapes suffisent pour obtenir, au sommet de l'atmosphère, une température apparente éloignée de moins de 0,1 K de sa valeur à l'issue de l'étape précédente.

Il s'agit maintenant de calculer les coefficients a_a et a_d pour les nuages et la pluie. Pour le modèle complet, ce coefficient a_a pour les nuages et la pluie sera ajouté au coefficient d'absorption pour les gaz, dont nous avons parlé au chapitre précédent, pour obtenir le coefficient d'absorption total d'une couche donnée.

3. COEFFICIENTS D'ABSORPTION ET DE DIFFUSION

Les nuages et la pluie [Berroir, 1986 ; Fleagle & Businger, 1980] sont composés de gouttes d'eau ou de glace que nous allons supposer sphériques.

La diffusion et l'absorption d'ondes électromagnétiques par une sphère diélectrique de rayon r a été modélisée par Mie [1908].

Pour une particule sphérique, le facteur d'efficacité pour l'absorption, noté x_a, peut être défini comme le quotient de la puissance absorbée par la particule par la puissance reçue sur sa surface apparente ; définition similaire pour la diffusion et x_d. Notons que ces facteurs peuvent être supérieurs à 1. Les résultats de Mie permettent d'écrire les x comme des sommes infinies de coefficients fonctions de n (indice de réfraction complexe relatif du milieu constituant la particule — eau ou glace pour nous) et de c = 2pr/l, l étant la longueur d'onde du rayonnement considéré dans le milieu environnant — l'air pour nous. Pour le calcul de ces facteurs d'efficacité, nous avons utilisé la procédure de Deirmendjian [1969] (voir Ulaby et al. [1981]).

Si la taille de la particule est très petite devant la longueur d'onde, on peut se placer dans l'approximation dite de Rayleigh¹. Dans ce cas la diffusion est petite devant l'absorption :

(5) [Note : - = ≈]

(6) [Note : - = ≈]

En ce qui nous concerne (vers 100 GHz), cette approximation n'est valable que pour les petites gouttes d'eau qui composent les nuages "légers".

A partir des facteurs d'efficacité pour une goutte, on peut calculer les coefficients d'absorption et de diffusion a_a et a_d pour un milieu donné (une couche en ce qui nous concerne), à condition de connaître la distribution des tailles des gouttes p(c). Les particules diffusantes sont supposées réparties aléatoirement dans le milieu et suffisamment éloignées les unes des autres, si bien qu'il n'y a pas de relation de phase cohérente entre les champs diffusés individuellement :

(7)

On a une relation similaire pour l'absorption [Ulaby et al., 1981]. Le coefficient d'absorption dû aux gouttes est ajouté au coefficient d'absorption dû aux gaz avant d'appliquer les relations (1), (3) ou (4).

La fonction p dépend de la modélisation du nuage ou de la pluie qu'il s'agit de simuler. Nous avons repris les modèles donnés par Deirmendjian [1969] et Ulaby et al. [1981] pour les nuages, Marshall & Palmer [1948] ou Sekhon & Srivastava [1971] (mentionnons aussi Laws & Parsons [1943]) pour la pluie. Les gouttes des nuages ont un rayon de l'ordre de la dizaine de microns et les gouttes de pluie un rayon de quelques millimètres. Les gouttes sont plutôt plus grosses pour les pluies plus fortes et les nuages plus lourds. La densité d'eau liquide dans les nuages est généralement comprise entre 0,1 et 1 g/m³ pour les modèles donnés par Ulaby et al., mais plutôt entre 1 et 10 g/m³ pour les modèles des mêmes nuages (!) donnés par Valley [1965].

Pour la pluie, si l'on néglige la température diffusée, mais non pas l'influence de la diffusion dans le calcul de l'extinction totale, on peut se contenter des formules semi-empiriques d'Olsen et al. [1978], du type a = a R^b, où R est le débit de pluie en mm/h et a et b dépendent de la fréquence.

La constante diélectrique complexe de l'eau est calculée d'après Manabe et al. [1987] ; pour la glace nous avons pris 3,15 pour la partie réelle [Ulaby et al., 1986] et 5.10^–3 pour la valeur absolue de la partie imaginaire, d'après les travaux du British Meteorological Office.

(Note de bas de page)

1 : C'est justement la diffusion Rayleigh, en l^–4, mais relativement aux ondes visibles et aux molécules de l'air (plutôt qu'aux gouttes d'eau) qui permet d'expliquer la couleur bleue du ciel et rouge du soleil couchant [Liou, 1980].

4. PROBLEMES ET QUESTIONS DIVERS

Beaucoup d'imprécisions et de facteurs inconnus pèsent sur un modèle de diffusion tel que celui que nous avons adopté.

– La polarisation est traitée de façon simplifiée. Le rayonnement atmosphérique n'est pas polarisé et la diffusion telle que nous la prenons en compte n'introduit aucune polarisation. Seul le rayonnement en provenance du sol peut donc introduire un certain taux de polarisation. Dans le calcul, pour les étapes où il s'agit d'obtenir une température diffusée, nous faisons la moyenne des températures de brillance horizontale et verticale incidentes (T_AP dans l'équation (2)) ; mais nous traitons indépendamment les deux composantes (T_AP dans l'équation (3)) lorsqu'il s'agit d'obtenir les températures transmises.

Pour un traitement plus complet de la polarisation, voir par exemple Liou [1980] pour les fondements, et Ishimaru et al. [1982] ou Huang & Liou [1983] pour des simulations aux longueurs d'onde millimétriques.

Le problème de la polarisation est, par certains côtés, lié à la forme des gouttes. Une goutte d'eau est sphérique jusqu'à une taille de 1 mm environ. Lorsque le diamètre augmente, la goutte s'aplatit. Les gouttes d'un diamètre supérieur à 5 mm ont toute chance de se briser [Pruppacher & Pitter, 1971]. En revanche les cristaux de glace ne sont pas du tout sphériques. Les mesures qui ont été faites à 37 GHz ont montré des différences atteignant 15 K, entre les températures de brillance verticale et horizontale (Grody, 1984). Le modèle de Wu & Weinman [1984] tient compte de la forme non sphérique des particules de glace. Ces mêmes auteurs soulignent d'ailleurs l'intérêt de disposer d'un radiomètre à deux polarisations pour étudier les nuages de grêle.

– Les nuages et la pluie sont considérés comme homogènes et les distributions de tailles des gouttes sont appliquées entre deux altitudes bien précises (pour la pluie, l'altitude haute est à peu près celle de l'isotherme 0° C), ce qui représente évidemment une approximation "brutale". D'autre part les distributions de tailles sont le reflet d'une moyenne de conditions différentes et sont souvent en désaccord avec une situation réelle prise individuellement. Enfin, les écarts sont importants entre les résultats obtenus, dans les mêmes conditions, pour différentes distributions (Marshall & Palmer et Sekhon & Srivastava : figure 1 [Prigent-Benoit, 1988]).

– Nous ne savons pas s'il faut forcer ou non à la saturation, voire à la sursaturation, la concentration en vapeur d'eau dans un nuage [Szejwach et al., 1981].

– On peut hésiter à donner à la température de la pluie une valeur constante tout au long de sa chute (c'est ce que nous avons supposé) ou la valeur locale du milieu traversé (la vitesse limite de chute, en cm/s, est voisine du rayon de la goutte en mm [Sauvageot, 1982]).

– Il y a beaucoup d'incertitude sur la valeur de la partie imaginaire de la constante diélectrique de la glace. Weinman [1988] choisit 2,8.10^–3 et Wilheit et al. [1982] 1,8.10^–3 ; voir aussi la compilation de Warren [1984]. Les particules de glace diffusent beaucoup plus que les gouttes d'eau (la différence vient justement de la partie imaginaire de la constante diélectrique). Il s'agit surtout de diffusion vers l'arrière, ce qui fait qu'un sondeur passant au-dessus d'un nuage de glace voit la température de brillance baisser car le rayonnement provenant du sol est renvoyé vers le bas alors que le fond du ciel à 3 K est réfléchi vers le haut. Le modèle de Weinman [1988] prédit des chutes de "plusieurs degrés" pour des cirrus, pour les fréquences de Météosat.

– Notre modèle est un modèle "plans parallèles". Nous ignorons toute limitation latérale de l'étendue des nuages. Cela signifie d'une part que le pixel vu par le sondeur est entièrement nuageux (et composé des mêmes nuages), et d'autre part et de façon imagée que toutes les températures diffusées ne peuvent sortir du complexe nuageux ou y rentrer qu'à sa base ou à son sommet. La première limitation peut être écartée en divisant le pixel en zones claire et nuageuse et en faisant la moyenne pondérée des températures de brillance obtenues indépendamment, mais pour le deuxième point il faut un traitement plus élaboré comme celui de Kummerow & Weinman [1988].

– Les itérations que nous opérons pour le calcul des températures diffusées fournissent en quelque sorte une simulation de diffusions successives. Est-ce équivalent à un traitement de la "diffusion multiple" [Ishimaru et al., 1982] telle qu'on l'évoque surtout dans le domaine des télécommunications ?

Agrandir

Figure 1 : température de brillance de l'atmosphère marine suivant le taux et le type de pluie.

5. QUELQUES SIMULATIONS

On pourrait lancer énormément de simulations pour connaître l'effet des nuages et des précipitations suivant les fréquences, l'opacité des canaux, le contenu en eau, en glace, l'altitude des nuages, l'émissivité du sol, etc. Phalippou et al. [1989] ont d'ailleurs présenté de nombreuses simulations pour les canaux de Météosat, avec un modèle de transfert radiatif différent du notre. Voir aussi les tables données par Chédin et al. [1986 (a)].

Sous quelle forme convient-il de produire les résultats : températures de brillance ou fonctions de poids ? Comme nous allons le voir, les fonctions de poids sont quelquefois profondément modifiées par un nuage alors qu'il n'y a quasiment pas de variation de température apparente correspondante, certains effets se compensant. Mais, du point de vue de l'inversion, c'est quand même la variation de température qui est le facteur important pour juger de la perturbation apportée par le nuage.

Nous avons pris pour exemple une fréquence d'AMSU-A et une fréquence de Météosat. La figure 2 montre les fonctions de poids des fréquences centrales des canaux AMSU-5 (53,596 GHz) et Météosat 3– (117,45 GHz). Nous avons choisi ces deux canaux car le sommet de leur fonction de poids est le même : on peut donc comparer les effets des nuages et de la pluie suivant la fréquence. On remarque d'abord que la fonction de poids du premier comporte deux maxima locaux. Cette particularité est assez rare. Une explication ici est peut-être à chercher dans le fait que la fréquence en question est la fréquence centrale d'une raie de O₂.Voir les formules II.B.-(7), (8), (13) et (14) : loin du centre de la raie, f est proportionnel à g donc à P ; le produit fr est donc proportionnel à P² ; au contraire, pour n = n_r, f est inversement proportionnel à P et fr varie donc peu avec l'altitude. Ce dernier cas est donc bien différent du cas plus habituel où la fréquence est éloignée du centre de la raie.

Agrandir

Figure 2 : fonctions de poids (atmosphère claire).

On remarque ensuite que la fonction de poids de Météosat est plus large vers son sommet, ce qui gênera quelque peu l'inversion, comme nous l'avons signalé dans la partie I.

La figure 3 (attention au changement d'échelle verticale !) montre les fonctions de poids calculées pour les mêmes fréquences et la même atmosphère mais avec un nuage de type cumulus congestus (de 1600 à 2000 m d'altitude, 0,8 g/m³ d'eau liquide [Ulaby et al., 1981], taux de vapeur d'eau laissé à sa valeur pour une atmosphère standard). On voit que l'effet de ce nuage est nettement plus sensible pour la fréquence la plus haute. Pour ce qui est des températures de brillance, on passe de 249,24 K (et 8,9 dB d'atténuation) à 248,01 K (12,7 dB) pour Météosat, et de 247,15 K (15,2 dB) à 247,05 K pour AMSU. Les températures reçues baissent car l'émission chaude du sol (corps noir) est atténuée par le nuage plus froid (ce serait le contraire pour une visée vers la mer). Les écarts sont faibles, mais on peut noter que l'écart enregistré pour Météosat est environ 12 fois plus important que l'écart pour AMSU. A ces fréquences et vu la taille moyenne des gouttes d'eau (20 mm), l'approximation de Rayleigh est assez bonne ; le facteur d'efficacité pour la diffusion dépend énormément de la longueur d'onde (en l⁴) et c'est l'une des raisons qui expliquent le fort rapport des écarts.

Agrandir

Figure 3 : fonctions de poids (avec nuage).

Enfin la figure 4 montre le cas du même nuage avec une pluie de 10 mm/h (à 0° C, entre le sol et l'altitude où la température atteint 0° C, avec une distribution de gouttes de Marshall & Palmer). L'effet sur la fonction de poids est très fort. Les températures de brillance tombent à 246,60 K (32,5 dB) pour Météosat et 246,66 K (28,2 dB) pour AMSU. Le rapport des écarts n'est plus que de 5. Le traitement complet de Mie était nécessaire.

Agrandir

Figure 4 : fonctions de poids (avec nuage et pluie).

Ces simulations concernaient des canaux assez opaques. Les effets sur les températures sont beaucoup plus importants pour des canaux fenêtres, ou des canaux dont le pic de la fonction de poids est dans le nuage ou au-dessous. Les perturbations sont renforcées (et généralement de signe opposé) pour une visée sur la mer. Ainsi à 110 GHz, sur la mer, le nuage précédent élève la température de 30 K.

En ce qui concerne les nuages de glace, pour que notre modèle fournissent des baisses de températures de brillance comparables aux 100 K rapportés par Wilheit et al. [1982] à 92 GHz (Gasiewski [1988] a même mesuré des chutes de 200 K pour des canaux peu opaques vers 118 GHz), il faut choisir un nuage de 2 km d'épaisseur (altitude 6000 m par exemple) dont le contenu en eau est de l'ordre de 0,5 g/m³ avec un rayon moyen de gouttes de 180 mm.

En résumé, il est certain que les fréquences proches de 118 GHz sont nettement plus touchées par les nuages et la pluie que les fréquences vers 55 GHz. Pour l'estimation d'un profil de température en ciel couvert, c'est fâcheux. Mais les optimistes [tel Gasiewski et al., 1987] rétorqueront que l'estimation de paramètres nuageux et d'altitudes et débits de pluie sera facilitée !

Sommaire Précédent Suivant Accueil