B. QUASI-OPTIQUE
Résumé — Ce long chapitre est consacré à la présentation de quelques éléments quasi optiques utilisables dans les radiomètres millimétriques. Nous rappelons tout d'abord les grandes lignes de la théorie des faisceaux gaussiens et les définitions de rayon, waist et rayon de courbure. Nous passons ensuite rapidement sur les éléments de réception et focalisation : cornets (de Potter ou scalaires), lentilles et miroirs. La section suivante, plus fournie, est consacrée au filtrage. Nous décrivons, en premier lieu, des plaques dichroïques à trous (filtres passe-bas) en insistant sur la mesure de leurs performances. Puis nous abordons les grilles de fils métalliques parallèles, qui constituent des polariseurs. A cette occasion sont soulignés quelques détails relatifs à la phase du facteur de réflexion. Par couples, ces grilles peuvent être employées pour réaliser des filtres de type Fabry-Pérot, dont nous rappelons la manière de calculer la réponse en transmission ou en réflexion. Quelques paragraphes évoquent les techniques de couplage quasi optique. Enfin, la dernière section traite de la rotation de polarisation. Nous présentons quelques calculs et tests relatifs à un appareil en apparence très simple, constitué par une grille de fils métalliques parallèles et par un plan conducteur placé un quart de longueur d'onde derrière la grille.
1. INTRODUCTION
Généralement, le rayonnement récolté par une antenne est concentré sur un cornet prolongé par un guide. Si nécessaire, on sépare dans le guide plusieurs "voies" menant à autant de mélangeurs. Mais, plus la fréquence est élevée, pire sont les affaiblissements provoqués par ces dispositifs séparateurs de fréquence ou de polarisation et, dans une moindre mesure, par les guides eux-mêmes (l'atténuation théorique est d'environ 0,1 dB par cm vers 180 GHz pour un guide WR5 [Saad et al., 1971]).
Le rôle des éléments appelés quasi optiques est de réaliser le maximum de fonctions, après le renvoi des ondes par le réflecteur primaire et avant de concentrer les ondes sur les cornets. Nous verrons en effet que ces éléments sont moins affaiblissants que leurs homologues en guide métallique. L'emploi du terme optique vient, en particulier, de la ressemblance des éléments en question avec ceux utilisées en optique : miroirs, lentilles par exemple 1 ; les conditions sont cependant différentes : les dimensions des éléments dans le domaine radio ne sont pas très grandes devant la longueur d'onde, contrairement aux cas habituels dans le domaine visible.
Parmi les fonctions réalisables, il y a le filtrage des bandes de fréquence, le traitement de la polarisation, le couplage des fréquences du signal et de l'oscillateur local vers le même cornet d'entrée d'un mélangeur, la concentration et le guidage des faisceaux.
Les inconvénients les plus évidents de ces dispositifs sont leur encombrement, les difficultés d'alignement, les problèmes liés à leur spatialisation.
Après d'autres, Goldsmith [1982] a décrit la théorie et les applications pratiques du domaine quasi optique. Nous nous inspirons beaucoup de sa présentation pour la suite de notre exposé.
Quand on recherche une solution y à l'équation d'onde obtenue à partir des équations de Maxwell, on aboutit à une onde plane lorsqu'on se limite à une dépendance en z (direction de propagation) et en t (temps). D'autres solutions, plus réalistes, peuvent être identifiées à des modes de propagation. Pour l'un de ces modes, appelé fondamental, la variation de l'amplitude du champ dans toute direction orthogonale à la direction de propagation a une forme gaussienne. En omettant le terme dépendant du temps eiwt, l'expression précise de ce mode gaussien est :
 (1)
(1)
A, w0 : constantes
r = (x2 + y2)1/2 : distance à l'axe de propagation
w(z), R(z) : fonctions lentement variables en z
l : longueur d'onde
k = 2p/l.
w est appelé le rayon (radius en anglais) du faisceau. Son minimum, w0, est le rayon au niveau de la taille, ou mieux de l'étranglement (waist) du faisceau, qui est placé arbitrairement à z = 0 :
 (2)
(2)
Les surfaces de phase constante sont sphériques ; R(z) est leur rayon de courbure :
 (3)
(3)
Revenons à l'expression (1). L'amplitude du champ dans un plan orthogonal à z est bien gaussienne, d'après la première exponentielle. La distance de l'axe à laquelle le champ électrique est égal à 1/e de sa valeur au centre (sur l'axe) est w(z). La densité de puissance en fonction de la densité au centre est (module du champ élevé au carré) :
![]() (4)
(4)
A grande distance du waist (c'est ainsi que nous l'appellerons), l'angle d'ouverture du faisceau, c'est-à-dire l'angle asymptotique de croissance du rayon, est :
 (5)
(5)
Quand le rayon du waist est grand, le faisceau est faiblement divergent (quasi parallèle).
La figure 1, tirée de Martin [1982], illustre la distribution de puissance d'un faisceau gaussien au voisinage de son waist.
Figure 1 : faisceau gaussien.
L'intérêt d'étudier la solution gaussienne à l'équation d'onde est le suivant : des cornets très classiques, que nous allons évoquer dans la section suivante, produisent un diagramme de rayonnement gaussien. En outre, on montre que si un faisceau est initialement gaussien, il reste gaussien lorsqu'il se propage sur l'axe d'un système optique. Mieux, un faisceau isolé tend naturellement à devenir gaussien.
Cependant, pour conserver au faisceau des caractéristiques bien connues et contrôlées, il ne faut pas que les systèmes optiques en question tronquent (trop) le faisceau, et introduisent (trop) de diffraction [Dickson, 1970]. Or, pour ces systèmes quasi optiques, la diffraction est toujours menaçante car les dimensions des objets par rapport à la longueur d'onde ne sont pas très élevées. On considère généralement qu'un diamètre de quatre fois le rayon du faisceau est suffisant pour éviter des effets néfastes. Des valeurs plus précises sont données par Belland & Crenn [1982].
A ce propos, calculons le rapport de la puissance perdue, si l'on tronque le faisceau par une ouverture circulaire de rayon r1, sur la puissance totale incidente :
 (6)
(6)
Ce rapport est donc égal à la densité de puissance au bord de l'ouverture par rapport au centre. Autrement dit, si l'on tronque le faisceau à –n dB du centre, le rapport de la puissance perdue à la puissance incidente est aussi de –n dB. Pour r1 = 2w (règle précédente), n vaut environ 35.
Nous allons donc présenter ou simplement évoquer quelques éléments réalisant les fonctions de focalisation et réception, filtrage, rotation de polarisation, couplage. Nous nous étendrons surtout sur deux éléments : la plaque dichroïque métallique à trous, à propos de laquelle nous présenterons en détail les méthodes de mesure en quasi-optique, et un rotateur de polarisation, étudié et testé. Le lecteur insatisfait des renseignements recueillis dans les parties les moins développées tirera un grand profit de la lecture attentive de la thèse de C. Prigent-Benoit [1988], ou d'autres ouvrages majeurs déjà cités en référence. Les articles de Prigent et al. [1988 (b)] ou Abba et al. [1987 (b)] sont plus concis.
(Note de bas de
page)
1 : L'utilisation de ces techniques n'est pas réservée aux domaines millimétrique et submillimétrique, comme le prouvent par exemple les alimentations périscopiques des antennes de télécommunication de 30 m de diamètre, fonctionnant à 4/6 GHz ; ces tehniques sont aussi employées en infrarouge.
2. FOCALISATION ET RECEPTION
2.a. Cornets
Le cornet est le dernier élément d'une chaîne quasi optique (peut-il être qualifié lui-même de quasi optique ?). Il réalise la transition entre la propagation en espace libre et la propagation guidée.
Les cornets pyramidaux sont faciles à fabriquer à haute fréquence, mais leurs diagrammes de rayonnement manquent de symétrie dans les plans E et H, ne sont pas gaussiens et ont de forts lobes secondaires. On préfère utiliser soit des cornets dits de Potter, soit des cornets dits scalaires.
Les cornets de Potter réalisent la combinaison des modes TE11 et TM11 d'un guide circulaire [Potter, 1963] : en anglais on les appelle dual-mode. Ils sont assez faciles à réaliser, ont un diagramme de rayonnement bien gaussien, des lobes secondaires bas (souvent au-delà de –30 dB), mais ils souffrent de la faiblesse de la largeur de leur bande passante.
Les cornets scalaires [Thomas, 1978], qui ont une bande utile plus large, sont plus élaborés. Les parois intérieures sont calculées pour imposer des conditions aux limites identiques pour les deux polarisations du champ électrique, produisant ainsi un diagramme de rayonnement symétrique avec des lobes secondaires très bas. Ces parois sont cannelées (ou rainurées, ou rainées, mais transversalement, et non longitudinalement ; en anglais : corrugated), d'où la vague relation entre l'allure d'un de ces cornets et ce qui est suggéré par l'étymologie de scalaire. Plus la fréquence est élevée, plus la réalisation d'un tel cornet est difficile, à cause de ces rainures dont la profondeur et le pas sont de l'ordre d'un quart de longueur d'onde. Les procédés de fabrication comprennent la technique dite d'électroformage : du cuivre est déposé par électrolyse sur un mandrin en aluminium, en quelque sorte "négatif" dans sa forme par rapport au cornet final ; le mandrin est ensuite dissous. Cette technique est d'ailleurs utilisée abondamment pour la fabrication d'autres éléments à très hautes fréquences comme les structures des mélangeurs ou multiplicateurs classiques.
Signalons qu'à des fréquences supérieures à 300 GHz, on n'utilise quelquefois même plus de cornet classique, et l'on reçoit directement les ondes sur un mélangeur qualifié alors de quasi optique, le whisker faisant office d'antenne.
2.b. Lentilles
Nous avons vu que la taille d'un faisceau croît avec l'éloignement du waist. D'autre part, les éléments de traitement du signal que nous voulons placer avant le cornet, et que nous décrirons dans les sections suivantes, fonctionnent généralement mieux lorsqu'ils sont situés au waist du faisceau (taille plus petite, front d'onde plan). Il nous faut donc des éléments pour focaliser les faisceaux, restreindre leur taille tout au long de leur cheminement dans le système quasi optique, et finalement les concentrer sur les cornets.
L'élément le plus simple est la lentille, comme en optique géométrique. Ici, le matériau est un diélectrique, le téflon par exemple. Le calcul de la forme de la lentille peut être fait comme en optique géométrique, sauf que les distances sont remplacées par les rayons de courbure R. On trouve, dans la littérature [Goldsmith, 1982 ; Dickson, 1970], les formules nécessaires pour calculer la distance focale de la lentille en fonction de la distance et du rayon voulus du waist en sortie, ou les distances des waists de part et d'autre d'une lentille de distance focale donnée lorsqu'on veut augmenter ou diminuer d'un facteur précis le rayon du waist du faisceau. Nous citons ici la formule générale de Dickson, les notations étant celles de la figure 2, f étant la longueur focale de la lentille et fF = pw02/l.

Figure 2 : propagation d'un faisceau gaussien aux abords d'une lentille.
 (7)
(7)
Avec cette formule, on se ramène facilement aux cas particuliers : d1 = 0, f = ¥ (pas de lentille), d1 = 0 (waist au niveau de la lentille), d2 = f (alors w2 = fl/pr0 est indépendant de d1). On peut aussi retrouver les relations donnant les lieu et rayon du waist en sortie. En particulier, le rayon maximal du waist en sortie, et donc la plus forte ressemblance de l'onde de sortie avec une onde plane, sont atteints pour d1 = f ; ce waist maximal est situé à la distance f de la lentille, quelle que soit la longueur d'onde, ce qui est très intéressant pour la conception d'un système large bande.
Citons aussi la formule suivante [Goldsmith, 1982 (par exemple)], plus classique mais moins générale, où l'on voit bien la ressemblance avec l'optique géométrique ("1/p + 1/p' = 1/f ") et le rôle des rayons de courbure donc de la diffraction qui n'est pas négligée ; dans cette expression, les indices "2" correspondent au waist en sortie de la lentille et non plus, comme dans la formule précédente, à un point quelconque sur l'axe en sortie de la lentille :
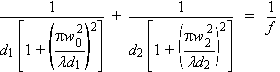 (8)
(8)
L'affaiblissement subi par le signal à la traversée de la lentille est peu élevé. C'est plutôt la réflexion à la surface qui pourrait atténuer le signal de façon trop gênante. On diminue fortement cette réflexion par l'usage d'une couche adaptatrice à la surface de la lentille. Une solution est de creuser des cannelures circulaires de profondeur voisine d'un quart de longueur d'onde (adaptation "l/4" entre l'air et le diélectrique).
2.c. Miroirs
Un miroir ellipsoïdal peut être considéré comme deux lentilles accolées, la distance focale de chacune étant la distance entre le foyer adéquat de l'ellipsoïde et le centre de la partie de la surface du miroir éclairée par le faisceau.
Sur les lentilles, les miroirs ont l'avantage de ne présenter quasiment pas d'atténuation, ni de limitation de bande passante, et de permettre de construire des systèmes de réception plus compacts en dirigeant les faisceaux dans les directions voulues. Cependant ils ne doivent pas être utilisés avec un angle d'incidence trop grand, en particulier pour des questions de transmission de la polarisation croisée.
3. FILTRAGE
Les types de filtre réalisables en quasi-optique sont nombreux. Non exhaustivement, on peut distinguer les filtres "simples", constitués par une lame unique qui a des propriétés différentes suivant la fréquence ou la polarisation, des filtres de type Fabry-Pérot, qui associent plusieurs lames simples pour augmenter la sélectivité.
Les filtres simples sont des réseaux de fils métalliques, de trous percés dans une plaque métallique, de motifs imprimés sur une lame diélectrique, etc. Le filtre est un obstacle presque transversal pour le faisceau incident, et divise ce dernier en deux (s'il n'y a pas de diffraction) faisceaux, l'un transmis sans (trop) de modifications, l'autre réfléchi. Comme il est recommandé de prendre pour diamètre de l'élément au moins quatre fois le rayon du faisceau, il vaut mieux placer le filtre au niveau du waist si l'on souhaite limiter l'encombrement.
Pour les réseaux de motifs imprimés, voir Arnaud & Pelow [1975] et Holah [1982] (ce dernier aussi pour les filtres Fabry-Pérot). Nous parlerons un peu plus loin des grilles de fils métalliques, avant la présentation du principe des filtres Fabry-Pérot. Nous commençons par présenter les plaques métalliques percées, ce qui nous donnera l'occasion d'exposer le genre de mesures que l'on fait dans le domaine quasi optique.
3.a. Plaques dichroïques
Introduction
On qualifie de dichroïque (terme emprunté à l'optique) une plaque métallique percée d'un réseau de trous (et aussi d'autres types de plaque) parce qu'une telle plaque constitue un filtre passe-bas et apparaît donc comme ayant des propriétés de transmission — des couleurs, en quelque sorte — bien différentes pour deux fréquences suffisamment éloignées l'une de l'autre.
Les trous sont généralement circulaires. On peut comprendre grossièrement comment cela fonctionne en considérant les trous comme des guides dont la fréquence de coupure serait aussi la fréquence de coupure de la plaque ; on essaie de placer le plus de trous possible ; plus la plaque est épaisse, plus les morceaux de guide sont longs et donc plus le filtre serait sélectif. En réalité, les choses ne sont pas aussi simples et l'épaisseur de ces plaques dépasse rarement une longueur d'onde.
Un calcul élaboré des performances de plaques à trous a été mené récemment par Letrou [1989], par le développement en harmoniques de Floquet du champ diffracté. Auparavant, les articles souvent abstrus de Chen [1973, par exemple] avaient ouvert la voie.
Ces plaques dichroïques à trous circulaires sont particulièrement utiles lorsqu'il s'agit de séparer des bandes de fréquence pas trop rapprochées, comme l'ensemble autour de 118 GHz et le canal vers 150 GHz (Météosat), ou ce même canal et l'ensemble autour de 183 GHz (Météosat ou AMSU).
Description des plaques testées
Nous avons mesuré les performances de deux plaques dichroïques, l'une en aluminium et l'autre en cuivre. Elles ont été calculées, pour Alcatel Espace, par l'ONERA (Office National d'Etudes et de Recherches Aérospatiales) à Toulouse, et réalisées par la société APMV (Vénissieux). Les détails des techniques de fabrication ne sont pas connus. La figure 3 donne les cotes et montre la disposition des trous.

Figure 3 : caractéristiques des plaques testées.
Une valeur approchée de la fréquence de coupure de ces filtres est donnée par la formule suivante, où nc est la fréquence de coupure du mode fondamental TE11 pour un guide circulaire de diamètre égal au diamètre des trous :
![]() (9)
(9)
Organisation des mesures
La figure 4 montre le banc de tests. Les divers éléments utilisés sont ceux qui étaient disponibles au moment des tests, compte-tenu des autres expériences en cours et des bandes de fréquence "historiquement" présentes au Laboratoire : celui-ci est ainsi mieux équipé en éléments WR6 (bande 110-170 GHz) et WR4 (170-260 GHz) qu'en WR5 (140-220 GHz).
Figure 4 : banc de tests.
Les mesures ont été faites sur un ensemble discret de fréquences, fournies par un carcinotron (générateur de fréquence) : 14 points répartis entre 149 et 195 GHz. Il aurait été possible de balayer en fréquence continûment et de visualiser la courbe atténuation / fréquence sur l'écran d'un analyseur scalaire Pacific Measurements ; mais la lecture aurait été moins précise et surtout le carcinotron ne délivrant pas une puissance constante sur toute la bande utile, on aurait risqué de subir pour certaines fréquences une non-linéarité du détecteur haute fréquence dans la chaîne de réception. La mesure point par point avec un "dB-mètre" permet une précision de lecture de l'ordre du dixième de dB. Grâce à l'atténuateur étalonné, à la sortie du carcinotron, on peut se placer toujours au même niveau de puissance, et vérifier la linéarité du détecteur. On s'affranchit des problèmes d'ondes stationnaires en recherchant à chaque mesure un maximum détecté (en déplaçant l'ensemble de réception avec une vis micrométrique).
Chaque élément du banc est réglable en hauteur et orientable dans le plan horizontal. Les cornets sont, de plus, mobiles autour des deux axes horizontaux.
Le "fréquence-mètre" donne la valeur de la fréquence fournie par le carcinotron avec une précision de l'ordre du dixième de GHz.
Les guides rectangulaires entre le carcinotron et le doubleur de fréquence sont des WR10 (bande 75-110 GHz). Le doubleur est prévu normalement pour une fréquence de sortie de 150 GHz, ainsi que les lentilles. En fait, ces éléments ont des performances encore honorables à 190 GHz. La bande normale des éléments de réception est 110-170 GHz (WR6). Le détecteur fonctionne très bien pour des fréquences un peu plus hautes. Cependant les mesures ont été faites jusqu'à 195 GHz (limite de rendement du doubleur), et la fréquence de coupure du premier mode parasite d'un guide WR6 est voisine de 182 GHz. Mais les tests étant "relatifs" (on mesure la différence dans les puissances reçues avec et sans l'élément testé), on peut penser que l'effet de la propagation éventuelle de modes secondaires est supprimé par le processus de mesure.
Les mesures ont été faites avec des angles d'incidence de 10, 20, 30 degrés en transmission et de 20 et 30 degrés en réflexion (les simulations théoriques n'ont été fournies que pour 20 degrés). Quelques résultats complémentaires pour des angles de 15 et 25 degrés ne sont pas repris ici.
Des ennuis avec le doubleur
(whisker déconnecté puis impossibilité après un nouveau contact de retrouver
des propriétés minimales au-dessus de 178 GHz ; déficience également du
doubleur de remplacement) ont empêché d'obtenir des mesures en mode TM et des
mesures de polarisation croisée. Les
résultats présentés ici ne concernent donc que le mode TE. Pour celui-ci,
la direction de polarisation du champ électrique est orthogonale au plan
d'incidence, défini par la direction de propagation et la normale à la grille
(figure 5). Ainsi, sur la figure 4, le champ ![]() est toujours vertical.
est toujours vertical.

Figure 5 : modes TE et TM.
En revanche tous les tests ont été faits pour deux orientations de la plaque, c'est-à-dire pour deux alignements possibles des trous avec le champ électrique (figure 6). Bien sûr ces alignements sont définis modulo 60°. Les simulations de l'ONERA semblent ignorer la différence entre ces deux configurations.

Figure 6 : alignement des trous.
La taille du faisceau incident sur la plaque est difficile à connaître précisément. En approchant un absorbant vers le centre de la plaque, successivement de différents côtés, jusqu'à obtenir une déviation de l'aiguille du dB-mètre (en général, dans le sens d'une plus grande atténuation !), on peut évaluer la grandeur de la zone éclairée de la plaque. Cette zone avait environ 1 à 1,5 cm de diamètre, ce qui fait que le faisceau "voyait" une centaine de trous (les simulations supposent sans doute une infinité de trous).
Résultats
– Influence de l'orientation des trous :
Voir les figures 7 et 8. Cette influence est quasiment nulle pour 10° d'incidence. A 20° elle est encore très faible : 2/3 des mesures montrent une différence entre les deux orientations inférieure ou égale à 0,1 dB, soit la précision de lecture sur le dB-mètre. A 30°, en revanche, elle est beaucoup plus sensible, surtout pour les hautes fréquences.
Pour les figures 9 à 11, nous avons fait la moyenne des valeurs obtenues sur les deux orientations.
– Influence de l'angle d'incidence :
Voir les figures 9 et 10. Les performances sont excellentes à 10°, très bonnes à 20°, très dégradées à 30°. Rappelons que les bandes de fréquence qui nous intéressent sont 175,3-191,3 GHz pour la transmission et 1 GHz centré à 150 ou 157 (voire 166) GHz pour la réflexion (aussi bien pour Météosat que pour AMSU). Il faudrait donc utiliser ces plaques avec une incidence inférieure ou égale à 20° ou à la rigueur 25°, mais pas au-delà : après 25° la chute des performances est rapide.
– Influence du métal :
Comparer les figures 9 et 10 et voir la figure 11 (la dernière). Les différences sont légères, et presque nulles dans la bande transmise. Les pertes 1 dans la bande réfléchie à 157 GHz sont plus faibles pour la plaque en cuivre : 0,4 dB contre 0,8 dB pour la plaque en aluminium. La fréquence de coupure de la plaque en cuivre semble être 0,5 à 1 GHz au-dessus de celle de la plaque en aluminium (on le voit bien sur la figure 11, pour les fortes atténuations). A signaler que les cotes sont exactement les mêmes pour les deux plaques.
– Comparaison avec la théorie et remarque sur la fréquence de coupure :
Voir la figure 11. Les courbes théoriques dessinées sont issues des données de l'ONERA. Les résultats du programme de C. Letrou (communication personnelle, 1989) sont très proches de ces courbes, mis à part une remontée vers 10 dB des pertes en réflexion, autour de 190 GHz. L'accord des mesures avec la théorie n'est pas totalement satisfaisant, surtout vers 170 GHz, ce qui n'est pas gênant, et au-delà de 186 GHz, ce qui dégrade les résultats qu'on pouvait espérer pour la bande transmise. La raison de cette dernière différence est peut-être à chercher dans le matériel utilisé pour les mesures, comme cela a été évoqué précédemment. En revanche le comportement de la plaque de cuivre en réflexion est très proche de la théorie.
En comparant les pertes mesurées des plaques aux alentours de 175 et 191 GHz, il paraît raisonnable de proposer pour AMSU-B une plaque avec une fréquence de coupure un peu plus haute : 2 ou 3 GHz au-dessus. Cela diminuerait les pertes moyennes pour la bande transmise et pour la bande réfléchie : 0,3 dB au lieu d'environ 0,5 dB pour un canal à 157 GHz ; et dans le cas d'une fréquence réfléchie de 166 GHz, on pourrait limiter les pertes autour de cette fréquence à 1,5 dB (au lieu de 3 dB avec les plaques présentes).
– Comparaison avec d'autres réalisations :
Comparées avec d'autres plaques de réalisation moins soignée testées précédemment à Meudon, ces plaques offrent des performances remarquables. La différence est probablement due à la qualité du poli et surtout à la précision de réalisation des trous (1 micron sur le diamètre d'après le constructeur). Les défauts constatés sur d'autres plaques étaient : trous non perpendiculaires à la plaque, de diamètre différent suivant le côté de la plaque, imparfaitement alignés ou pas assez serrés.
Source d'une plus grande surprise est la comparaison avec les performances annoncées des plaques présentement sur le marché. Ainsi les plaques proposées par la société Millitech [1986] ont-elles des pertes de l'ordre de 1,5 dB dans la bande transmise (90 à 110 GHz pour une fréquence de coupure de 81 GHz).
– En résumé, pour un projet comme AMSU-B :
Pour un angle d'incidence inférieur ou égal à 20°, les pertes sont en moyenne de 0,5 dB (0,2 dB à 150 GHz), et toujours inférieures à 1 dB. Les performances se dégradent lamentablement et rapidement à partir de 25°. Moyennant un angle d'incidence raisonnable, on peut dire en conclusion que la faisabilité de la séparation des canaux 17 / 18-20 d'AMSU-B est parfaitement démontrée.
(Note de bas de
page)
1 : Voir la première note du chapitre D.
Figures 7 à 11 (pages suivantes) : performances mesurées des
plaques dichroïques.
Toutes les courbes expérimentales sont tracées par interpolation à partir de
mesures ponctuelles.
3.b. Grilles polarisantes
Les grilles polarisantes ont des facteurs de transmission et de réflexion dépendant de la polarisation. La grille la plus simple, et celle que nous allons présenter, est un réseau de fils métalliques parallèles. Si ceux-ci sont suffisamment rapprochés, un champ électrique parallèle aux fils est presque complètement réfléchi, et un champ électrique orthogonal est parfaitement transmis.
Plus précisément, il faut aussi tenir compte de l'épaisseur des fils et de la longueur d'onde. Larsen [1962] a présenté une revue de toutes les formules de la littérature. Voir aussi Marcuvitz [1951] pour des cas plus généraux, en particulier pour des fils à section non circulaire, ou des bandes métalliques minces ; plus récemment : Bliek et al. [1980], Pauchard [1980], Mok et al. [1979], Chambers et al. [1980]. Souvent les auteurs expriment leurs résultats en décrivant la grille comme une impédance shuntant une ligne de transmission en espace libre, ou plus généralement comme un quadripôle inséré dans la ligne en question. Dans ce genre de représentation, l'impédance et le facteur de réflexion sont très simplement reliés.
En recombinant les champs diffractés par les fils on aboutit, pour la valeur de l'impédance d'une grille dont les fils sont parallèles au champ électrique incident, à une somme infinie dont tous les termes sauf un sont négligeables sous certaines conditions. D'où la valeur approchée du facteur de réflexion pour l'énergie :
 (10)
(10)
p : période du réseau
a : diamètre d'un fil
j : angle d'incidence (angle entre la normale à la grille et la direction de propagation).
Pour un champ électrique orthogonal aux fils, le facteur de réflexion sous incidence normale est :
 (11)
(11)
Pour cette dernière formule, il y a incertitude, suivant les auteurs, sur le facteur au dénominateur : 2 ou 4/3. L'influence de l'angle d'incidence n'est pas non plus très explicite.
Les expressions (10) et (11) sont valables pour a << p << l. On a par conséquent, dans ce cas, R// ≈ 1 et R^ ≈ 0 : la grille est un polariseur.
Nous venons de voir le cas d'un champ parallèle ou orthogonal aux fils. Pour des directions d'incidence et de polarisation complètement arbitraires, se reporter à Wait [1955]. En résumé, et pour une grille parfaitement polarisante : soit une onde d'incidence et de polarisation quelconque ; sa composante orthogonale aux fils (elle est définie de façon unique) est complètement transmise car elle n'induit aucun courant dans les fils ; son autre composante (orthogonale à la composante précédente) est parallèle à la projection orthogonale des fils sur un plan perpendiculaire à la direction de propagation de l'onde, et cette composante est complètement réfléchie.
Les applications de ces grilles polarisantes sont nombreuses. En choisissant correctement l'orientation relative des fils de plusieurs grilles placées l'une derrière l'autre, Saleh [1974] puis Chen [1980] ont conçu des filtres passe-bande, le premier pour une onde sous incidence normale, le second sous incidence oblique. On peut également réaliser des filtres Fabry-Pérot, des dispositifs de couplage et des rotateurs de polarisation.
Remarque sur les lobes de réseau
Chaque fil diffracte l'onde incidente dans toutes les directions. Pour simplifier, considérons une onde dont la direction de propagation est orthogonale aux fils : soit j son angle d'incidence. Les ondes diffractées se retrouvent en phase pour des directions y telles que (figure 12) :
![]() (12)
(12)

Figure 12 : réseau diffractant.
Il y a toujours au moins deux solutions à l'équation (12), obtenues pour n = 0. Ce sont y = j : onde transmise ; y = p – j : onde réfléchie. Quand il n'y a pas d'autre solution réelle, les autres ondes sont évanescentes. S'il y a d'autres solutions réelles, alors de l'énergie est effectivement émise dans les directions associées, et l'on parle de lobes de réseau. Pour éviter les lobes de réseau, il faut donc que :
![]() (13)
(13)
Soit, en définitive :
![]() (14)
(14)
Signalons qu'il y a sans doute une erreur de signe dans la formule similaire (4) de Larsen [1962].
En résumé, pour p < l/2, il n'y a jamais de problèmes.
Remarques sur la phase du facteur de réflexion
Les expressions (11) et (12) concernaient des facteurs de réflexion en puissance. Jusqu'ici rien n'a été dit sur la phase de ces facteurs. Considérons une surface partiellement réfléchissante (la discussion qui suit n'est pas limitée aux grilles de fils tendus). Soit r et t les facteurs de réflexion et de transmission complexes, pour une incidence et une polarisation données. Soit r et t les phases respectives, et R et T les facteurs pour l'énergie. On écrit [Ulrich, 1967 (a) ; Saleh, 1974] :
r = ïrïeir ïrï2 = R
t = ïtïeit ïtï2 = T (15)
Nous allons supposer que la plaque partiellement réfléchissante est très mince devant la longueur d'onde. Par continuité du champ électrique de part et d'autre de la plaque :
1 + r = t (16)
Si nous supposons de plus que la plaque est sans pertes (fils parfaitement conducteurs par exemple) :
R + T = 1 (17)
Après quelques lignes de calcul, (16) et (17) amènent aux relations suivantes, qui montrent que phases et amplitudes des facteurs de réflexion et transmission sont étroitement liés :
![]()
![]()
![]()
![]() (18)
(18)
e = ± 1 (c'est le même pour sinr et sint).
On remarque alors (par exemple en calculant cos(r – t)) que r – t = ± p/2 : les ondes réfléchie et transmise sont déphasées de p/2. Dans le plan complexe, r décrit le cercle de centre (–1/2, 0) et de rayon 1/2 (figure 13). Pour une grille parfaitement polarisante, r = –1.

Figure 13 : phases des facteurs de réflexion et de transmission pour une grille inductive.
Ulrich [1967] appelle inductive une grille pour laquelle e = 1 et capacitive une grille pour laquelle e = –1 1. Ces termes sont issus de la représentation de la grille comme une impédance shuntant la ligne de transmission : si l'impédance en question a sa partie imaginaire qui croît avec la fréquence, la grille est dite inductive ; et inversement pour une grille capacitive.
Il convient cependant de bien préciser une chose. On peut choisir de définir l'expression complexe d'une onde électromagnétique sous deux formes différentes :
![]()
Cette onde se propage suivant la direction et le sens de l'axe Ox, k étant le module du vecteur d'onde, w la pulsation de l'onde (monochromatique), t le temps et i2 = –1. Ces deux expressions ont, bien sûr, la même partie réelle :
![]()
La convention généralement employée (et qui est souvent implicitement spécifiée dans la littérature ; plus rarement explicitement, comme Ulrich et al. [1963]) est de prendre pour facteur dépendant du temps e+iwt. Certains auteurs (par exemple Born & Wolf [1980] ou Renault [1980]) choisissent plutôt e–iwt. En reprenant les équations traditionnelles sur la propagation, on constate alors que, dans ce dernier cas, la constante diélectrique complexe doit s'écrire e = e' + ie" au lieu de e' – ie" qui correspond à e+iwt (e' et e" réels positifs). De même, la constante de propagation est g = a – ib au lieu de a + ib (a et b réels positifs). En allant plus loin, et si l'on gardait la même convention e–iwt pour la représentation complexe des grandeurs électromagnétiques, l'impédance complexe deviendrait –iLw pour une self et i/Cw pour une capacité : en fait dans ce cas, l'impédance serait conjuguée de celle obtenue avec la représentation classique. Ces considérations deviennent importantes lorsqu'on traite de la réflexion d'une onde, si le facteur de réflexion a une phase différente de 0 ou p, comme nous allons le montrer. Soit un champ se propageant suivant Ox ; nous cherchons l'expression exacte du champ réfléchi par une surface quelconque. Avec la convention e+iwt et si le facteur de réflexion complexe est r = ïrïeir, le champ réfléchi est :
![]() (19)
(19)
Notons que le signe devant le terme kx est devenu positif, car la propagation, après réflexion, se fait dans le sens des x négatifs.
Si la convention est e–iwt, aussi bien pour les ondes que pour les impédances, le facteur de réflexion est r' = ïrïeir', avec r' = –r, et l'on a :
![]() (20)
(20)
Mais enfin, si la convention est e–iwt pour les ondes mais reste e+iwt pour les impédances (c'est le cas chez Renault [1980]), il faut écrire :
![]() (21)
(21)
Les trois expressions (19) à (21) sont alors égales.
Des réflexions similaires s'appliquent au facteur de transmission.
(Note de bas de
page)
1 : En fait, Ulrich traite surtout des grilles "à deux dimensions", c'est à dire obtenues en croisant à angle droit deux réseaux de fils parallèles pour former un treillis, qui est inductif. Il n'est alors plus question de propriétés polarisantes. La structure complémentaire, c'est-à-dire composée de pavés conducteurs (supportés par un film transparent) est capacitive. Ulrich [1967 (b)] fait d'une ou plusieurs de ces grilles un filtre passe-bas, fonctionnant en transmission pour les structures capacitives et en réflexion pour les structures inductives. Pour un article plus récent et d'autres références, voir Lee et al. [1982]. La structure capacitive est un exemple parmi les réseaux de motifs imprimés que nous avons évoqués au début de la section.
3.c. Interféromètre Fabry-Pérot
Rappels théoriques sur la construction classique
Les filtres de type Fabry-Pérot sont particulièrement recommandés lorsqu'il faut séparer deux bandes de fréquence très proches. Dans la version classique, deux lames partiellement réfléchissantes sont placées l'une derrière l'autre sur l'axe de propagation du signal, la distance entre les deux lames étant judicieusement choisie. Le facteur de réflexion de chaque lame est proche de 1. Le calcul du facteur total de transmission ou de réflexion est l'expression de l'interférence des signaux, transmis ou réfléchis à l'infini par les lames (on parle, en anglais, de multiple beam interference). La figure 14 montre le cas le plus simple : dans le vide ou dans l'air, deux lames minces partiellement réfléchissantes (par exemple deux grilles à fils tendus telles que nous venons de les étudier) sont écartées d'une distance d et sont attaquées sous l'angle d'incidence q par un signal de longueur d'onde l ; r et t étant les facteurs complexes de réflexion et de transmission d'une lame, pour l'amplitude.

Figure 14 : interféromètre Fabry-Pérot.
Nous choisissons e+iwt pour la représentation temporelle du champ incident, supposé de polarisation linéaire (champ électrique parallèle aux fils). Chaque onde émergeant à droite du dispositif, considérée dans un plan quelconque orthogonal à la direction de propagation, a pour déphasage par rapport à l'onde précédente (qui a subi un aller-retour de moins entre les lames) :
![]() (22)
(22)
Si l'on parvient à combiner toutes les ondes transmises, le champ incident voit alors son amplitude multipliée par :
![]() (23)
(23)
A la lumière de la dernière remarque de la sous-section précédente, le lecteur scrupuleux se convaincra de la validité du signe négatif à l'intérieur des exponentielles exprimant les déphasages 1.
Le facteur de transmission global, T, est le carré du module du facteur multiplicatif précédent. On trouve facilement, avec r = ïrïeir et R = ïrï2, la formule d'Airy :
 (24)
(24)
Le facteur de réflexion global du dispositif est naturellement R = 1 – T.
En fonction de la fréquence, la courbe de transmission de cet élément est une succession périodique de pics d'autant plus pointus et de vallées d'autant plus larges et creusées que R est proche de 1. La période de cette succession est, d'après (22), c / 2dcosq : les pics sont d'autant plus rapprochés que la distance séparant les lames est grande. Au sommet des pics (f º 2r modulo 2p), la transmission est égale à 1 quel que soit R — cela paraît surprenant a priori —, mais elle n'est jamais nulle dans les vallées.
Les utilisations d'un interféromètre de Fabry-Pérot sont diverses dans les domaines millimétrique et submillimétrique [Goldsmith, 1982] et encore plus variées dans le domaine visible. Un tel élément permet de séparer deux bandes de fréquence très proches. Par exemple dans le projet Météosat, le canal à 110 GHz, étroit, pourrait être transmis alors que la large bande de fréquences autour de 118,75 GHz (de 114,55 à 122,95 GHz) serait réfléchie. Une application voisine est le rejet de la bande image et la transmission de la bande signal, avant un mélangeur.
(Note de bas de
page)
1 : Le déphasage f n'est l'expression que de la différence "géométrique" de chemin optique. Le déphasage introduit par les réflexions et transmissions est évidemment pris en compte par les termes r et t.
Autres constructions et couplage quasi optique
Dans un autre registre, qui n'est plus à proprement parler du filtrage, citons aussi le couplage des fréquences issues de l'oscillateur local et de l'antenne avant entrée dans le mélangeur. Plutôt que des lames à faces parallèles, on emploie un assemblage de miroirs parfaitement et partiellement réfléchissants. Un des dispositifs les plus populaires utilise quatre lames disposées en carré [Gustincic, 1977] (figure 15 [Goldsmith, 1982]), et peut aussi être employé comme filtre.
Figure 15 : Fabry-Pérot de Gustincic.
Ouvrons ici une parenthèse. Tous les appareils de couplage quasi optique n'emploient pas des techniques de type Fabry-Pérot. Un des coupleurs les plus utilisés est l'interféromètre décrit par Payne & Wordeman [1978], qui se présente sous la forme d'un double chevron constitué de deux miroirs parfaitement réfléchissants et de deux lames partiellement transparentes, ou la version un peu plus élaborée bien qu'antérieure d'Erickson [1977]. Ce type d'élément est dérivé du principe de Mach-Zender [Fedoseev, 1982]. Egalement très utilisée, la construction de Martin & Puplett [1969], dans laquelle des grilles polarisantes sont associées à des miroirs en équerre, est analysée dans le détail par Lambert & Richards [1978] et Martin [1982].
Le fonctionnement de tous ces dispositifs s'explique facilement par le calcul. Il faut parfois se rappeler que les faisceaux réfléchis et transmis par une lame semi-transparente sont déphasés de p/2. Pour le Fabry-Pérot de Gustincic, les formules (23) et (24) sont toujours valables, mais f est alors égal à 8pd / l√2, d étant la distance entre deux lames parallèles.
Interféromètres Fabry-Pérot réels
L'interféromètre décrit dans la partie théorique est un instrument idéal. Il y a plusieurs choses que nous avons négligées.
Parlons d'abord des effets appelés en anglais walk-off. Il y a l'effet walk-off géométrique et l'effet walk-off par diffraction (parfois appelé seulement effet de diffraction). Le premier est simplement le reflet de l'incidence non normale. Sur la figure 14, on voit bien que les ondes émergeant du dispositif sont décalées les unes par rapport aux autres. En optique on les rendraient concourantes au moyen d'une lentille. Ici, cependant, il faut se rappeler que les faisceaux gaussiens sont assez larges : nous n'avons représenté sur la figure 14 que les axes de ces faisceaux. En sortie, ces faisceaux non coaxiaux se chevauchent, et le couplage électromagnétique est d'autant meilleur (et l'affaiblissement du signal par walk-off géométrique d'autant plus faible) que le chevauchement est important. Il convient donc d'attaquer un dispositif Fabry-Pérot à lames parallèles par un faisceau large devant l'espacement des lames, et sous un angle d'incidence assez faible. N'oublions pas cependant que les signaux émergeant de l'appareil sont des sommes infinies de signaux décalés régulièrement, et par conséquent qu'il est toujours impossible de récupérer toute l'énergie. En revanche, le montage de type Gustincic, où les lames sont toujours attaquées avec une incidence de 45°, ne connaît aucun effet walk-off géométrique.
Le deuxième problème est celui engendré par la croissance "naturelle" d'un faisceau gaussien. Ce dernier ne peut être considéré comme parallèle qu'au voisinage de son waist, et sur une courte distance. Au fur et à mesure qu'un faisceau subit des réflexions dans l'interféromètre, son extension latérale est de plus en plus différente de celles des autres faisceaux avec lesquels il va devoir se combiner à la sortie du dispositif. Il ne peut donc plus y avoir couplage optimal. Dans la construction de Gustincic, on peut résoudre le problème en donnant à l'un des deux miroirs la forme concave appropriée pour, en quelque sorte, focaliser à chaque tour les faisceaux encore en course dans l'interféromètre [Pickett & Chiou, 1983].
Goldsmith [1982] donne les formules élémentaires pour calculer les facteurs de couplage de deux faisceaux gaussiens dans le cas général, tandis qu'Arnaud et al. [1974] analysent en détail les effets walk-off des Fabry-Pérot.
Jusqu'à présent nous n'avons évoqué que des configurations de lames semi-réfléchissantes dans l'air (ou le vide). Mais il peut être utile, conseillé (pour réduire les pertes par walk-off [ibidem]), ou plus facile, d'utiliser un diélectrique. Par exemple les lames à faces parallèles de la figure 14 pourrait être des motifs métallisés sur une plaque diélectrique. Dans ce cas le calcul est un peu plus compliqué : se reporter à Born & Wolf [1980] et à Goldsmith [1982]. Il faut en particulier distinguer les facteurs de réflexion et de transmission de chaque face suivant le sens de passage de l'onde (du diélectrique vers l'air ou inversement), faire intervenir l'indice de réfraction n dans la différence de marche de deux signaux, et éventuellement tenir compte des pertes diélectriques.
Enfin, il est possible de placer plus de deux lames partiellement réfléchissantes pour accroître la raideur et élargir la bande passante de ces filtres interférentiels [Van de Stadt, 1987].
Une dernière remarque
L'optimisation des paramètres d'un filtre Fabry-Pérot n'est pas chose aisée. La figure 16 montre les solutions possibles pour un exemple précis. Il s'agit de séparer une bande étroite vers 229 GHz d'une bande de 850 MHz située 3,2 GHz plus haut, le facteur de transmission du filtre pour la bande qu'il réfléchit devant être inférieur à –20 dB. Les trois courbes traduisent trois possibilités ; nous avons laissé ces courbes décalées les unes par rapport aux autres pour mieux les distinguer. La première courbe représente la solution la plus naturelle : elle consiste à placer la bande réfléchie au creux d'une vallée ; ainsi le facteur de réflexion R d'une lame n'a pas à être trop élevé : 0,83. Les deux autres courbes présentent des pics de transmission plus séparés, obtenus en rapprochant les lames, mais pour assurer le niveau de rejet voulu (–20 dB), il a fallu augmenter la valeur de R. L'avantage des solutions 2 et 3 est d'augmenter la largeur de la bande transmise ; celle-ci (bande à 3 dB) est indiquée sur la figure 16 pour chacune des trois solutions.
Figure 16 : optimisation d'un filtre Fabry-Pérot.
Il y a une autre chose qui entre alors en ligne de compte : la précision du réglage de l'écart entre les deux lames. D'après (22), la précision relative sur le placement d'un pic est liée à la précision relative de l'écartement des lames :
![]() (25)
(25)
Quand, à R constant, on divise par deux la distance entre les lames : on éloigne deux pics consécutifs d'un facteur deux, on double la bande passante, mais on doit être deux fois plus exigeant sur la précision de placement des lames (équation (25)). Si la bande à transmettre est très inférieure à la bande passante du Fabry-Pérot, cette contrainte sur la marge de tolérance paraît annulée par le doublement de la bande passante. Cependant comme la contrainte sur la séparation des bandes force à augmenter la valeur de R et par conséquent à réduire la bande passante, la précision nécessaire est finalement accrue. Mais encore faut-il savoir quelle est la source de l'imprécision de placement des lames. Si c'est la dilatation thermique qui les écarte ou les rapproche de façon gênante, cette dilatation sera deux fois moins forte si d est divisé par deux, relançant l'intérêt du rapprochement des lames !...
Sur la figure 16 sont précisées les marges de tolérance sur d, lorsque la bande à transmettre, large de 100 MHz, doit être complètement inclue dans la bande à 3 dB transmise.
4. ROTATION DE POLARISATION
4.a. Introduction
Il est souvent intéressant de connaître la polarisation du signal observé. Nous avons vu, en particulier, que les composantes horizontale et verticale du rayonnement issu d'une surface quelconque était différentes, contrairement à celles du rayonnement atmosphérique. L'analyse des deux composantes peut donc aider à la discrimination entre les effets atmosphériques (nuages, pluie) et la contribution propre de la surface. D'ailleurs, certains des radiomètres pour la télédétection mentionnés dans la partie I, comme SMMR, recueillaient deux composantes orthogonales.
L'analyse de la polarisation requiert a priori l'usage de deux chaînes de réception. Par exemple, en ce qui nous concerne, il faudrait pour chaque canal de Météosat doubler tous les éléments à partir du mélangeur ou peut-être même du cornet. Une solution moins encombrante serait de pouvoir se servir de la même chaîne de réception pour les deux composantes du signal, en contraignant l'ensemble à tourner périodiquement de 90° : solution très lourde. Il est beaucoup plus élégant de faire tourner la polarisation du signal avant son entrée dans la chaîne de réception, et de garder celle-ci complètement fixe. Cette opération est très facilement réalisable en quasi-optique.
Il faut cependant reconnaître que la quantité d'information recueillie en analysant successivement les deux composantes du signal est moindre que celle obtenue en doublant le nombre de récepteurs. Cela se traduit par une dégradation de la sensibilité radiométrique d'un facteur √2, pour une même zone observée pendant le même temps (d'après I.A.-(7), le temps effectif d'observation étant divisé par 2).
Nous avons réalisé et testé un "rotateur" de polarisation quasi optique, très simple, composé d'une grille de fils tendus placée à un quart de longueur d'onde d'un miroir métallique [Abba et al., 1987 (a) ; Prigent et al., 1988 (a)]. C'est la théorie et les performances de cet instrument que nous allons bientôt décrire. Amitay & Saleh [1983] ont proposé des rotateurs de polarisation fonctionnant en transmission (et non en réflexion comme le nôtre), composés d'au moins trois grilles polarisantes parallèles, dont les fils sont orientés dans des directions différentes. Aagesen [1957] a déjà présenté la rotation de polarisation par une grille placée devant un miroir, mais ses calculs sont compliqués et peu clairs. Wait [1954] a étudié théoriquement la réflexion d'une grille devant un plan conducteur, en particulier dans le dessein de réaliser une surface absorbante en augmentant la résistance des fils. Pour une, ou plutôt des définitions de la polarisation croisée, voir Ludwig [1973].
4.b. Principe de l'analyse de la polarisation
Nous supposons pour l'instant que la grille est parfaite (R// = 1, R^ = 0, déphasage de p pour la réflexion, comme sur un miroir), et qu'elle reçoit une onde monochromatique sous incidence quasi normale. Un plan parfaitement conducteur est placé derrière la grille, parallèlement et à la distance d = (2k + 1) l/4, k étant un entier naturel. Le récepteur est sensible à la polarisation verticale.
Le champ incident total ET (nous notons ici, dans le texte, les vecteurs en caractères gras, sans flèche ; sur les schémas, nous les coiffons d'un accent circonflexe) est la somme de deux composantes orthogonales Ehorz and Evert qui vont devoir être détectées l'une après l'autre.
– D'abord, les fils sont orientés verticalement (figure 17) ou (respectivement) horizontalement . La composante verticale du champ incident est réfléchie par la grille ou (resp.) par le miroir, et est reçue par le récepteur avec un changement de phase égal à p ou (resp.) 2p.
Figure 17 : réception de la composante verticale sans rotation.
– Ensuite, on fait tourner la grille dans son plan pour orienter les fils à 45° (figure 18). La composante horizontale du champ total est divisée en deux vecteurs d'amplitude égale. L'un, E//, est réfléchi par la grille ; le second, E^, passe à travers elle, est réfléchi par le miroir et se combine avec E// avec un retard de phase relatif égal à p. Par conséquent le champ électrique résultant Erés est vertical et donc détecté.
Figure 18 : rotation et réception de la composante horizontale.
Il suffit donc de monter ce dispositif sur un moteur permettant de faire alterner les deux positions de la grille, pour analyser successivement les deux composantes orthogonales d'un signal quelconque.
Une autre fonction de cet appareil peut être la rotation d'un champ électrique de polarisation linéaire connue. Si q est l'angle que fait un fil avec la direction de polarisation du champ incident, on vérifie rapidement que cette polarisation subit une rotation de p + 2q.
A partir de maintenant, nous considérerons uniquement le cas d'une rotation de (±) 90°.
4.c. Quelques calculs
Bien entendu cet appareil, fondé sur des principes de réflexion, ne peut être utilisé avec une incidence nulle comme nous venons de le supposer.
Soit le repère orthonormé direct (O, x, y, z). Un champ électrique de polarisation horizontale, Einc = E0 x, frappe maintenant la grille verticale sous incidence oblique (voir la figure 19). Sa direction (orientée) de propagation –z fait l'angle p – j avec la normale n de la grille : n = – x sinj + z cosj (–90° < j < 90°). Le récepteur est toujours supposé détecter une polarisation verticale. Les fils de la grille sont inclinés de l'angle q par rapport au plan horizontal (X, Z). La projection orthogonale d'un fil dans le plan (X, Y) fait l'angle a avec l'axe X :
![]() (26)
(26)
Figure 19 : grille sous incidence oblique.
Le champ incident Einc peut s'exprimer comme la somme des champs E1 et E2 :
![]()
![]() (27)
(27)
E2 est perpendiculaire à la projection orthogonale des fils sur le plan (X, Y) et perpendiculaire aux fils eux-mêmes. E2 est donc complètement transmis. E1, qui est orthogonal à E2, est complètement réfléchi (voir 3.b). Ce champ réfléchi par la grille, s'exprime, d'après les lois de Snell-Descartes :
![]()
![]()
![]() (28)
(28)
Quant au champ E2 réfléchi par le miroir, il devient, après un aller-retour entre la grille et le miroir :
![]()
![]() (29)
(29)
Nous avons omis la dépendance en temps eiwt. f est le déphasage dû à l'aller-retour :
![]() (30)
(30)
(On peut vérifier que le champ ERm est orthogonal aux fils et donc bien transmis à travers la grille au retour.) Si nous supposons qu'il y a couplage parfait entre entre les deux champs émergents (pas d'affaiblissement walk-off), le champ résultant est :
![]() (31)
(31)
Ce champ a une polarisation elliptique. Le récepteur reçoit sa composante sur Y :
![]() (32)
(32)
La fraction de la puissance totale incidente qui est reçue est donc :
 (33)
(33)
Si la distance d est réglée pour avoir un premier maximum de R à la fréquence n0 = c/l0, on a d = l0 / 4cosj (équation (30)) et, pour la fréquence n : f = pn/n0. Finalement, (26) et (33) donnent :
 (34)
(34)
On obtient R = 1 avec n = n0 et :
ïtgqï = cosj , soit a = ± 45° (35)
La partie restante 1 – R de la puissance incidente est restituée orthogonalement à Y (polarisation croisée).
Cas d'une grille imparfaite
Nous supposons maintenant R// ≠ 1, mais pour simplifier l'étude, nous conservons l'hypothèse R^ = 0. En fait, d'après les formules (10) et (11), on a R^ << 1 – R// dans la plupart des cas. En reprenant les relations (18) et les notations relatives aux grilles, nous écrivons les facteurs de réflexion et de transmission pour la polarisation parallèle aux fils :
r = – cos r eir
t = – i sin r eir (36)
En tenant compte des multiples réflexions entre la grille et le miroir, et pour a = 45° (i.e. pour une rotation de 90° du champ incident), on aboutit après quelques lignes de calculs à la nouvelle expression traduisant la transformation du champ E1 par le dispositif :
 (37)
(37)
Comme R^ = 0, le champ E2 est traité par l'appareil comme précédemment. Nous récrivons la relation (29) avec a = 45° :
![]() (38)
(38)
Cette fois-ci le facteur R est plus difficile à calculer. On obtient finalement :
 (39)
(39)
Il est alors facile de montrer qu'on obtient encore R = 1 si sinf = tgr. Or, la grille étant inductive, r est légèrement inférieur à p. Cette relation montre donc que l'effet d'une grille imparfaite (i.e. r ≠ p) peut être totalement corrigé en accroissant un peu la distance entre la grille et le miroir (il fallait auparavant f = p, il faut maintenant f légèrement supérieur à p). Ce raisonnement est valable tant que ïtgrï ≤ 1, soit R// ≥ 0,5. On voit donc que le rotateur de polarisation peut théoriquement fonctionner parfaitement avec un piètre polariseur. Cependant il est hautement préférable d'avoir un grille très réfléchissante, pour limiter l'effet walk-off. A ce propos, il faut par ailleurs que le faisceau à traiter soit large devant la distance d, pour ne pas souffrir de l'effet walk-off géométrique.
Une dernière remarque : le rotateur doit être placé près du waist du faisceau (ou sur le chemin d'un faisceau peu divergent ou convergent), pour que l'angle d'incidence j, qui détermine l'angle d'orientation des fils q, soit à peu près constant sur toute l'étendue transversale du faisceau.
4.d. Résultats expérimentaux
Un prototype conçu pour fonctionner autour de 100 GHz a été réalisé en cuivre (fils et plaque). La distance entre les fils et la plaque peut être ajustée entre 0 et 6 mm par vis et ressorts. Les caractéristiques de la grille sont p = 0,5 mm et a = 0,1 mm. D'après (10) et (11) on a donc, à 90 GHz, R^ ≈ 0,001, et pour 45° d'incidence, R// ≈ 0,99.
Nous avons utilisé un carcinotron couvrant la gamme 70-110 GHz ; le montage était semblable à celui présenté sur la figure 4. La position du rotateur par rapport au waist du faisceau était inconnue. Nous avons fait des mesures à différents angles d'incidence, mais surtout à 45°. Pour cet angle, la transformation d'un champ horizontal en un champ vertical est obtenue avec q = 35,3° ou 144,7° (relation (35), en convenant de prendre q positif).
La figure 20 présente la réponse du rotateur suivant les valeurs de q, la distance entre la grille et le miroir étant accordée pour n0 = 90 GHz. Le récepteur est sensible à la polarisation verticale, et l'on envoie un signal à 90 GHz de polarisation successivement verticale et horizontale. Il y a un très bon accord entre la théorie et les mesures. Les différences peuvent venir de défauts dans la grille (mauvaise planéité, pertes ohmiques sur les fils).
Figure 20 : puissance détectée suivant les valeurs de q et la polarisation incidente.
La figure 21 donne une idée de la bande d'utilisation du rotateur. Les cornets sont placés pour émettre et recevoir un signal à polarisation verticale. Le rotateur est fixé pour faire tourner la polarisation incidente de 90° (q = 35,3°). En conséquence, la courbe en pointillés montre la polarisation croisée engendrée par le système, soit, en théorie (n0 = 90 GHz) :
 (40)
(40)
L'accord des mesures avec la théorie est bon jusque vers –20 dB. Bien sûr, la théorie ne prend pas en compte la polarisation croisée introduite éventuellement par les cornets ou les lentilles.
Figure 21 : puissance détectée de la polarisation croisée suivant la fréquence.
La bande utile est plus étroite lorsque l'espacement est calculé et ajusté pour 3l0/4, 5l0/4, etc.
Des versions motorisées de ce rotateur sont mises en place sur le canal à 157 GHz de MARSS et sur la maquette du sondeur millimétrique de Météosat (chapitre E). La réalisation des grilles de fils tendus, confiée au Laboratoire de dispositifs infrarouges et micro-ondes à l'Université Paris VI, suit les principes décrits par Sentz et al. [1978].
Sommaire Précédent Suivant Accueil